Bases de données relationnelles et normalisation :
de la première à la sixième forme normale
Date de publication : 07/09/2008. Date de mise à jour : 14/07/2012.
Notes. Compléments
A. Tuples, relations, relvars (définitions)
A.1. Tuple (n-uplet), attribut
A.2. Relation, relvar
A.3. Note à propos de Tutorial D
B. Notation des opérateurs relationnels (Tutorial D)
B.1. Restriction
B.2. Projection
B.3. Rename
B.4. Jointure (naturelle)
B.5. Union, Intersection, Différence
B.6. EXTEND
C. Notes concernant la 1NF et la logique du 2e ordre
C.1. Univers du discours
C.2. Termes généraux
C.3. Concept de classe
C.4. Vers la logique du deuxième ordre : termes généraux considérés comme des objets
C.5. L'exemple de la généalogie et ses applications
C.6. Au sujet des RVA de Date et Darwen
D. La normalisation et le bonhomme NULL
E. Fermeture des dépendances fonctionnelles, axiomes d'Armstrong, ensemble irréductible
E.1. Fermeture d'un ensemble de dépendances fonctionnelles
E.2. Axiomes d'Armstrong
E.3. Application des axiomes, calcul de la fermeture des DF
E.4. Fermeture d'un ensemble d'attributs, l'algorithme du seau à dépendants
E.5. Inventaire des clés et surclés. Quelques observations.
E.5.1. La technique du rouleau compresseur
E.5.2. Cas des attributs ne figurant pas dans les dépendants des DF
E.5.3. Surclés n'ayant pas d'attributs en commun et utilisation de l'algorithme du seau
E.5.4. Clés oubliées
E.6. Ensemble irréductible de dépendances fonctionnelles
E.6.1. Ensembles de DF et redondances
E.6.2. Propriétés d'un ensemble irréductible de DF
E.6.3. Pluralité des ensembles irréductibles pour une relvar
E.7. Décompositions sans perte
E.7.1. Préservation du contenu de la base de données
E.7.2. Préservation des dépendances fonctionnelles
E.8. Conclusion
F. Identification relative versus identification absolue
F.1. Consommation des ressources physiques
F.2. Performance des applications
F.3. Le clustering selon DB2 for z/OS
F.4. L'identification relative au service de l'intégrité des données
Notes. Compléments
A. Tuples, relations, relvars (définitions)
A.1. Tuple (n-uplet), attribut
Étant donné une collection de types Ti (i = 1, 2, ..., n), non nécessairement tous distincts,
une valeur de tuple (tuple pour abréger) sur ces types — disons t — est un
ensemble de triplets ordonnés de la forme <Ai,Ti,vi>, dans lesquels Ai est un
nom d'attribut, Ti est un nom de type et vi est une valeur du type Ti, et :
- La valeur n est le degré de t.
- Le triplet ordonné <Ai,Ti,vi> est un composant de t.
- Le couple ordonnée <Ai,Ti> est un attribut de t, identifié de façon unique
par le nom d'attribut Ai (les noms d'attributs Ai et Aj sont les mêmes seulement si i = j).
La valeur vi est la valeur d'attribut de l'attribut Ai de t. Le type Ti est le
type d'attribut correspondant.
- L'ensemble {H} = {A1 T1, A2 T2, ..., An Tn} des attributs constitue
l'en-tête de t.
- Le type de tuple de t est déterminé par l'en-tête de t, et possède les mêmes
attributs (donc les mêmes noms d'attributs et mêmes types) et le même degré que ceux de t.
Le nom du type de tuple — défini au moyen du générateur de type TUPLE — est précisément :
TUPLE {A1 T1, A2 T2, ..., An Tn}
Où TUPLE désigne un générateur de type.
A.2. Relation, relvar
Une valeur de relation (ou relation) — appelons r cette valeur —
est constituée d'un en-tête et d'un corps tels que :
- L'en-tête {H} de r est identique à celui d'un tuple, tel que défini ci-dessus.
La relation r a les mêmes attributs (et donc les mêmes noms d'attributs et les mêmes types
de référence) et le même degré que cet en-tête.
- Le corps de r est un ensemble de tuples ayant tous cet en-tête ; le cardinal de cet
ensemble est le cardinal de r.
- Le type de relation de r est déterminé par l'en-tête de r et possède les mêmes
attributs (donc les mêmes noms d'attributs et mêmes types) et le même degré que cet en-tête.
Le type de r (et le nom du type de relation de r) est précisément :
RELATION {A1 T1, A2 T2, ..., An Tn}
Où RELATION désigne là aussi un générateur de type.
La relvar (abréviation de variable relationnelle) est une variable prenant pour valeurs des
relations dont le type est mentionné lors de la définition de la relvar. Exemple :

Figure A.1 - Relvar Membre
En SQL, la déclaration de la structure de la table Membre, homologue de la relvar Membre, pourrait être la suivante :

Figure A.2 - Table Membre
Signalons que la relvar dont nous parlons est plus précisément une relvar de base
(base (ou real) relvar), par contraste avec la relvar dérivée
(derived (ou virtual) relvar),
autrement dit la vue.
 |
En tout état de cause, le Modèle Relationnel ne comporte qu'un seul type de variable, à savoir la relvar.
|
A.3. Note à propos de Tutorial D
Le Modèle Relationnel de Données fut défini avec une grande rigueur (ce qui ne veut pas dire rigidité !)
par Codd à partir de 1969. Cette rigueur permet au Modèle d'évoluer (évolution, oui, révolution, non !) grâce
notamment au soin pris par Codd pour éviter la redondance, donc la complication. Les années passant, Date et
Darwen assistèrent à des dérives et à des critiques non fondées du Modèle, notamment concernant de prétendues
lacunes, ce qui les incita à remettre les pendules à l'heure. Ceci fut fait lors de la publication en 1998 de
leur ouvrage « Foundation for Object/Relational Databases, The Third Manifesto ».
A cette occasion, D & D
procédèrent à une remise à plat complète du Modèle, un peu à la manière de Russell et Whitehead avec les
Principia Mathematica. Ainsi, les concepts de tuple, de relation et relvar, sans oublier celui de type ont
été formulés avec le plus grand soin dans [Date 2006], ce qui les a conduits à définir un
langage approprié, Tutorial D.
D & D ont conçu Tutorial D en respectant les « Principles of good language design »
qui leurs sont chers :
|
« Tutorial D est un langage de programmation complet du point de vue du calcul, intégrant toutes
les fonctionnalités des bases de données. Nous n'avons pas voulu qu'il soit perçu comme doté de la
“puissance industrielle” ; Il s'agit plutôt d'un langage “jouet” dont l'objet principal est de servir de
support pour l'enseignement. En conséquence, ont été volontairement omises de nombreuses fonctionnalités
qu'exigerait un langage véritablement industrialisé. (L'extension du langage pour la prise en compte de ces
fonctionnalités serait un projet qui en vaudrait la peine, le transformant ainsi en ce qu'on pourrait appeler
Industrial D.) ... ». (Cf. [Date 2006], page 93).
|
Par «
langage de programmation complet du point de vue du calcul », on doit comprendre que des
applications entières
peuvent être ainsi développées, il ne s'agit pas seulement d'un « sous-langage » de données hébergé par
quelque langage hôte propre à fournir les possibilités de calcul nécessaires.
Tutorial D est langage « jouet » dans la mesure où rien n'est pris en compte
en ce qui concerne par exemple les sessions
et les connexions, les communications avec le monde extérieur (gestion des entrées/sorties, etc.),
ou la gestion des exceptions et des codes-retour.
Un langage vraiment relationnel, disons de la famille
D, peut très bien intégrer des fonctionnalités
indépendantes du Modèle Relationnel, dans la mesure où elles n'en pervertissent pas l'esprit. Par exemple,
D pourrait à l'instar de SQL proposer un générateur de type ARRAY ou MULTISET
(cf. [Date 2006], chapitre 10 / « RM Very strong suggestions », page 234),
mais en aucune façon
un concept en contradiction avec l'esprit du Modèle Relationnel tel que celui de pointeur
(exemple : type REF de SQL).
En effet, toute information, quelle qu'elle soit, doit être représentée dans la base de données
uniquement sous forme
de valeurs prises par les attributs, au sein de tuples dans les relations
(
Information Principle de Codd).
Pour les SGBD basés sur Tutorial D, voyez
http://www.thethirdmanifesto.com/
Si les liens ci-dessous sont toujours actifs au moment où vous lisez ces lignes, vous pourrez en tirer profit.
Chris Date raconte les débuts du Modèle Relationnel de Données :
Thirty Years of Relational: The First Three Normal Forms (By C.J. Date)
http://web.archive.org/web/20050307045933/www.intelligententerprise.com/db_area/archives/1999/993003/online2.jhtml
Thirty Years of Relational: The First Three Normal Forms, Part 2 (By C.J. Date)
http://web.archive.org/web/20050307044845/www.intelligententerprise.com/db_area/archives/1999/992004/online2.jhtml
Et aussi, concernant Date :
Normalization Is No Panacea :
http://web.archive.org/web/20030218095332/http:/www.dbpd.com/vault/9804date.htm
Etc. :
http://web.archive.org/web/20050426234346/www.intelligententerprise.com/authors/search_Date.jhtml
B. Notation des opérateurs relationnels (Tutorial D)
L'objet n'est pas de décrire ici l'ensemble des opérateurs de l'algèbre relationnelle, mais de
revoir certains d'entre eux dans le cadre du Modèle Relationnel, car leur notation (Tutorial D)
diffère quelque peu de celle dont on dispose en SQL.
Voir le mapping des opérateurs Tutorial D / SQL :
www.dcs.warwick.ac.uk/~hugh/CS252/CS252-TD-to-SQL.pdf
B.1. Restriction
La restriction permet, à partir d'une relation R, de produire une relation R′ ayant le même en-tête
que celui de R et dont le corps en est un sous-ensemble
(cardinal de R′ ≤ cardinal de R). L'opération met
en jeu une condition impliquant un ou plusieurs attributs de R et devant être vérifiée par chacun
de ses tuples.
La restriction est ainsi formulée :
R WHERE condition
Par exemple, en reprenant la base de données de la Figure 2.6 :
F WHERE Ville = "Paris" ;
|
est une restriction de F sur l'attribut Ville, auquel on applique la condition
d'égalité « Ville = "Paris" » :
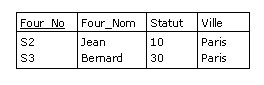
Figure B.1 - Résultat de la restriction
Traduction en SQL :
B.2. Projection
La projection permet, à partir d'une relation R, de produire une relation R′ dont l'en-tête
est un sous-ensemble de celui de R (degré de R′ ≤ degré de R)
et dont le cardinal est celui de R (ou inférieur si des redondances sont éliminées).
La projection est ainsi formulée :
R { X, Y, ..., Z }
expression dans laquelle X, Y, ..., Z sont des attributs de R.
Par exemple
est une projection de F sur les attributs Four_No et Statut :
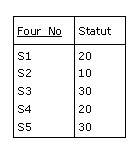
Figure B.2 - Résultat de la projection
Traduction en SQL :
B.3. Rename
L'opérateur Rename permet, à partir d'une relation R, de produire une nouvelle relation égale en valeur
(même corps), mais avec tout ou partie des noms des attributs ayant été renommés.
Par exemple, pour produire (au moins conceptuellement) une relation identique à la relation P de
la Figure 2.6, tout en renommant les attributs Piece_Nom et Poids respectivement en Libellé_Pièce
et Poids_Pièce :
P RENAME
(Piece_Nom AS Libellé_Pièce, Poids AS Poids_Pièce)
|
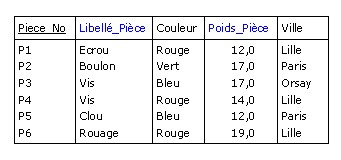
Figure B.3 - Résultat du RENAME
B.4. Jointure (naturelle)
Soit RA et RB deux relations dont les attributs sont respectivement les suivants
X1, X2, ..., Xm, Y1, Y2, ..., Yn
et
Y1, Y2, ..., Yn, Z1, Z2, ..., Zp
Y1, Y2, ..., Yn représentant les seuls attributs
ayant le même nom dans les deux relations. On observera que :
-
Après RENAME si nécessaire, aucun des attributs X1, X2, ..., Xm n'a le même nom qu'un des
attributs Z1, Z2, ..., Zp.
- Chaque attribut Yk (k = 1, 2, ..., n) est du même type dans les deux relations, par définition.
Résumons maintenant {X1, X2, ..., Xm}, {Y1, Y2, ..., Yn} et {Z1, Z2, ..., Zp}
respectivement par X, Y, Z. Alors, la jointure naturelle de RA et RB
RA JOIN RB
est une relation d'en-tête {X, Y, Z} et dont le corps est constitué de tous les tuples
{X x, Y y, Z z} tels que chacun de ces tuples apparaît dans RA avec X ayant la valeur x et Y
ayant la valeur y d'une part et apparaît dans RB avec Y ayant la valeur y et Z ayant la valeur z d'autre part.
Par exemple, dans le cas des relations F1 et P1 ci-dessous : X correspond à la paire
{Four_No, Four_Nom}, Y au singleton {Ville} et Z à la paire {Piece_No, Piece_Nom} :
.jpg)
Figure B.4 - Relations F1 et P1
La jointure naturelle
F1 JOIN P1
produit la relation :
.jpg)
Figure B.5 - Jointure naturelle des relations F1 et P1
Équivalent SQL :
B.5. Union, Intersection, Différence
Il n'y a rien de particulier à dire concernant les opérateurs UNION, INTERSECT, MINUS,
si ce n'est que les opérandes doivent être du même type (donc avoir exactement le même en-tête :
mêmes noms des attributs et mêmes types de référence pour ces derniers).
Soit donc F1 et F2 deux relations de même type :

Figure B.6 - Union des relations F1 et P1 : les opérandes sont du même type
L'union de F1 et F2 s'écrit
F1 UNION F2
et produit un résultat de même type :
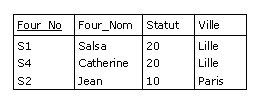
Figure B.7 - Résultat de l'union des relations F1 et P1
Équivalent SQL :
B.6. EXTEND
L'opérateur EXTEND permet, à partir d'une relation R de produire une relation dont l'en-tête est celui de R,
augmenté d'un attribut (liste d'attributs dans le cas général, se reporter à [Date 2006] et [Date 2010]).
La valeur prise par chaque tuple de la nouvelle relation pour cet
attribut est le résultat d'une opération portant sur les valeurs prises par les autres attributs
pour ce même tuple.
Plus précisément, la valeur de l'extension
EXTEND R ADD exp
AS Z
est une relation :
-
Dont l'en-tête est celui de R, étendu de l'attribut Z.
-
Dont le corps est constitué de tous les tuples t, tels que t est un tuple de R
étendu avec une valeur de Z résultant de l'évaluation de exp pour le tuple t.
L'en-tête de la relation R ne doit pas comporter d'attribut nommé Z et exp ne doit pas
mentionner Z. Le type de Z est celui de exp.
Exemple
Considérons la relvar des pièces :
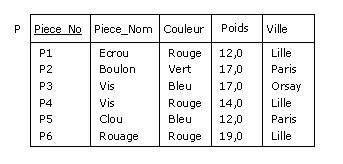
Figure B.8 - Relvar des pièces
Supposons qu'à partir de P, on veuille fournir une relation comportant le poids en grammes des pièces
(dans P, ce poids est exprimé en livres anglaises et une livre = 454 grammes). On utilise alors
ainsi l'opérateur EXTEND :
EXTEND P
ADD (Poids * 454) AS Poids_Grm
|
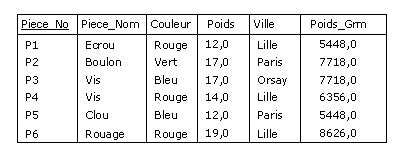
Figure B.9 - Extension de P (poids en grammes)
C. Notes concernant la 1NF et la logique du 2e ordre
Comme on l'a vu lors de l'étude la première forme normale (cf. paragraphe 2.1), Ted Codd avait écrit en 1969 :
|
Le calcul des prédicats du deuxième ordre est nécessaire (plutôt que celui du premier ordre)
parce que les domaines sur lesquels les relations sont définies peuvent à leur tour contenir
des éléments qui sont des relations.
|
Tandis qu'il se ravisait un an plus tard (cf. paragraphe 2.2) :
|
L'utilisation d'un modèle relationnel de données ... permet de développer un sous-langage
universel basé sur le calcul des prédicats. Si la collection des relations est en forme normale,
alors un calcul des prédicats du premier ordre est suffisant.
|
Et il montrait comment normaliser une relation contenant d'autres relations.
Indépendamment de ces considérations coddiennes, on peut se demander ce qu'est la logique
du 2e ordre. N'étant pas logicien, je me garderai de développer le sujet, mais, à la demande
de tel et tel relecteurs, me contenterai simplement de quelques indications, en me basant
essentiellement sur l'ouvrage Méthodes de logique [Quine 1972] de W.V.O. Quine, qui est
considéré comme l'un des plus grands philosophes américains du XXe siècle, sinon le plus grand.
C.1. Univers du discours
Quelques concepts importants sont d'abord à rappeler, tel que celui d'
univers du discours.
On doit ce concept à Augustus De Morgan, qui le présente dans un article de 1846,
On the Structure of the Syllogism,
puis dans son traité de 1847,
Formal Logic (page 55).
A l'époque, il utilise l'expression
Univers d'une proposition, qu'il abrège en
Univers.
En logique, l'univers du discours représente une collection d'objets, d'éléments dont nous sommes convenus
de partager la compréhension, sans chercher nécessairement à les énumérer tous. L'intérêt de cet
univers est qu'il permet, de façon décisive, de dépasser les limites de la stricte logique
aristotélicienne. Citons l'article de 1846, page 380 :
|
Writers on logic [...] give an indefinite negative character to the contrary, as Aristotle when
he said that not-man was not the name of anything. Let the universe in question be “man:”
then Briton and alien are simple contraries; alien has no meaning of definition except not-Briton...
|
La contribution d'A. De Morgan est capitale, ne serait-ce que parce qu'implicitement, elle
sous-entend le concept de Complémentaire, indispensable à la théorie des ensembles
(étant donné un sous-ensemble A d'un ensemble E,
on appelle complémentaire de A dans E
l'ensemble des éléments de E qui n'appartiennent pas à A).
En tout état de cause, nous pouvons parler de l'univers des membres de DVP. De même, un MCD,
un diagramme de classes, un MLD sont des exemples d'univers. Par le biais de l'univers du
discours nous convenons de ce dont nous parlons, tout en nous imposant de facto des limites :
si l'on parle de géométrie euclidienne, on se restreint par rapport à un univers plus vaste,
comprenant les géométries non euclidiennes, pour lesquelles les axiomes définis par Euclide
ne sont plus tous applicables. Et puis, nos capacités à raisonner ne sont pas infinies.
Quoi qu'il en soit, dans le cadre de la logique et pour reprendre la définition de Quine,
l'univers du discours est le parcours (range) d'objets x convenant à l'argument logique
que nous nous proposons de mener à bonne fin.
Par exemple, dans le contexte des bases de données, la table Membre des membres de
Developpez.com (cf. paragraphe 2.2) peut être considérée comme un univers de n-uplets que
l'on peut parcourir. Dans la notation du langage QUEL :
RANGE OF x
IS Membre
RETRIEVE (x
ALL)
|
(RETRIEVE (x ALL) peut être traduit par SELECT * en SQL).
C.2. Termes généraux
Parlons maintenant des termes généraux. A cet effet, considérons les objets de notre univers
des membres de DVP : Antoine, Bruno, Frédéric, Philippe, ... A la suite de Quine, pour dire,
de manière générale, qu'un membre de cet univers assure la fonction de modérateur nous utilisons
ce que l'on appelle un terme général :
Quelqu'un est modérateur.
On peut à cette occasion remplacer le pronom « quelqu'un » par une variable :
x est modérateur.
Et produire un schéma de phrase (dans lequel la lettre « F » symbolise le terme
général lui-même) :
Fx.
De même, pour dire, dans cet univers, qu'untel a la grande vertu d'être patient,
on utilise un autre terme général :
x est patient.
Ce que l'on peut symboliser une fois de plus au moyen d'un schéma de phrase :
Gx.
De tels schémas peuvent être combinés à l'aide de fonctions de vérité
(conjonction, disjonction, négation...) Ainsi, pour affirmer que quelqu'un est à la fois
modérateur et patient, on pourrait être est tenté d'écrire :
Fx . Gx
(Le point symbolise la conjonction : « Fx et Gx »).
Mais attention, il y a un piège à utiliser deux fois la variable « x »,
car en réalité, cette combinaison de schémas doit être lue ainsi :
Quelqu'un est modérateur et quelqu'un est patient.
Ce qui signifie tout à fait autre chose, par exemple qu'Antoine est modérateur et Bruno patient :
ça n'est pas parce qu'on a utilisé systématiquement « x » dans les schémas de phrases
que l'on peut en déduire que l'on parle de la même personne. Les termes « x est modérateur »,
« x est patient » représentent encore ce qu'on appelle des phrases ouvertes,
groupes de mots ni vrais ni faux, et qui n'attendent qu'une seule chose, être transformées
en phrases closes, c'est-à-dire contrôlées par des quantificateurs permettant cette fois-ci
de composer les schémas sans erreur d'interprétation et préciser si la variable « x »
y représente effectivement le même objet.
Ainsi, grâce aux quantificateurs universel « (∀x) »
et existentiel « (∃x) »
(Merci, M. Frege !), on peut enfin combiner des schémas de phrases pour symboliser,
sans ambiguïté, des compositions vérifonctionnelles de phrases (c'est-à-dire pouvant
être vraies ou fausses). Par exemple :
(∃x)(Fx . Gx)
Quelques modérateurs sont patients. (Le point symbolise la conjonction « et »).
(∃x)(Fx . ¬Gx)
Quelques modérateurs ne sont pas patients. (« ¬ » symbolise la négation).
(∀x)(Fx → Gx)
Tous les modérateurs sont patients. (La flèche symbolise le conditionnel « si ... alors »).
(∀x)(Fx → ¬Gx)
Aucun modérateur n'est patient.
Des variables telles que « x », « y », « z »,
etc., ne sont en fait que de
simples pronoms utilisés pour renvoyer aux quantificateurs.
Quand une variable est quantifiée, elle est dite liée, sinon elle est dite libre.
Pour reprendre l'exemple des modérateurs patients, dans l'expression
(∃x)(Fx . Gx)
la variable « x » est liée et l'on doit lire :
« Il y a au moins quelqu'un qui est à la fois modérateur et patient ».
Mais attention, si l'on écrit :
(∃x)(Fx) . Gx
le schéma « Gx » n'est plus sous le contrôle du quantificateur, et si la variable
« x » est liée dans « Fx », elle a été rendue libre dans « Gx ».
Autrement dit, cette combinaison aurait pu être écrite ainsi, de façon strictement équivalente :
(∃x)(Fx) . Gy
C'est-à-dire, dans les deux cas : « Il y a au moins un modérateur et, par ailleurs,
quelqu'un est patient ».
3lignes.jpg) |
Les termes généraux « x est modérateur » et « x est patient »
sont qualifiés de monadiques
car ils ne mettent en jeu qu'une seule variable. Mais un terme général peut être affecté de deux,
trois, n variables, auquel cas on dit qu'il est dyadique, triadique, n-adique (polyadique).
Par exemple « x est F à l'égard de y » peut être noté « Fxy » et
« x donne y à z » peut être noté « Gxyz ».
|
A titre d'exemple, comme le propose Quine, penchons-nous sur l'expression (dans laquelle sont mis
en jeu un terme général monadique et un terme général dyadique) :
(∀x)[Fx → (∃y)(Fy . Gxy)].
Si l'on interprète « Fx » comme « x est un nombre » et
« Gxy » comme
« x est plus petit que y », alors cette expression va signifier :
Tout nombre est tel qu'un nombre le dépasse.
De même, l'un des axiomes de l'identité est ainsi formulé :
(∀x)(∀y)(Fx . Gxy → Fy).
Où « Gxy » symbolise « x = y », et l'on peut du reste préférer
écrire simplement :
(∀x)(∀y)(Fx . (x = y) → Fy).
C.3. Concept de classe
Il est un concept qui ne nous est pas utile en logique du 1er ordre, celui de classe, mais qui
permettra ultérieurement de traiter de problèmes qui échappent à cette logique. La notion de
classe est une généralisation de la notion d'ensemble, mais pouvant aussi être perçue comme le
nom d'un terme général : de même que « est membre du Club des développeurs » est un
terme général, de même « DVP » peut être considéré comme le nom d'une classe.
En logique du 1er ordre, on n'a pas besoin de faire appel à la notion d'ensemble et à
l'appartenance d'un élément à un ensemble, mais rien n'empêche d'écrire « x ∈ DVP ».
S'intéresser aux propriétés communes aux membres de DVP, peut, si on le souhaite,
conduire à représenter ces propriétés par des classes et noter « x ∈ P »
le fait que l'objet x a la propriété P.
A la limite, un univers du discours U peut lui-même faire l'objet d'une classe universelle
Pu pour laquelle
on vérifierait la propriété universelle « est vrai de chaque objet ».
A partir de la table Membre (cf. paragraphe 2.2), créons maintenant des vues SQL correspondant
à des restrictions sur la localisation des membres :
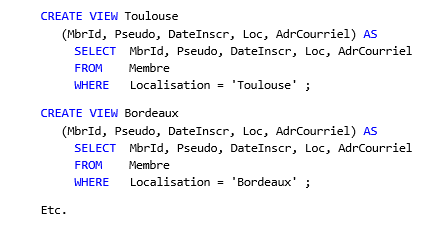
Ces vues sont des tables virtuelles, donc des relations, donc des ensembles, donc des classes.
Intéressons-nous à une classe en particulier, par exemple celle des Toulousains.
Pour utiliser QUEL une fois de plus :
RANGE OF x
IS Toulouse
RETRIEVE (x
ALL)
|
Instruction qui, comme on le sait, sera du reste transformée ainsi par le système relationnel :
RANGE OF x
IS Membre
RETRIEVE (x
ALL)
WHERE Localisation = 'Toulouse'
|
La variable « x » parcourt un univers que, pour les besoins de l'exemple,
on a spécifié et nommé « Membre ». On pourrait aussi définir des variables
« α », « β », etc.,
afin de pouvoir parcourir un univers U_Localisation
dont les éléments seraient les vues, donc les classes Toulouse, Bordeaux, etc.,
c'est-à-dire une vue qui serait une restriction portant sur la vue
INFORMATION_SCHEMA.TABLE_CONSTRAINTS fournie par le système relationnel (cf. la norme SQL) :
RANGE OF α
IS U_Localisation
RETRIEVE (α
ALL)
|
C.4. Vers la logique du deuxième ordre : termes généraux considérés comme des objets
Examinons maintenant l'expression :
(∀x)(∀y)[(x = y) ←→
(∀F)(Fx ←→ Fy)]
(« ←→ » symbolise le biconditionnel
« si et seulement si »).
Ce qui se lit : Quels que soient x et y, x est égal à y
si et seulement si quel que soit le terme général F, il revient au même d'appliquer
ce terme général à x ou à y. Initialement, les objets sur lesquels portait la
quantification étaient Antoine, Bruno, etc. (voire des nombres), bref, des objets concrets
et maintenant, on quantifie sur des termes généraux, abstraits, considérés à leurs tour comme
des objets alors qu'ils représentent des propriétés des objets par ailleurs quantifiés
(par exemple, être membre du Club des développeurs). On change de niveau, on entre en fait
dans le domaine du 2e ordre.
Quantifier sur des termes généraux ne se fait pas à la légère. Procéder ainsi pourrait prêter à
confusion et Quine attire notre attention à ce sujet. Dans ce qui suit, je fais encore référence
à son ouvrage, plus précisément au chapitre 43, « Les classes ».
Supposons que la lettre schématique « F » tienne la place du terme général
« aimer les chats ». La traduction en logique (du 1er ordre) de l'énoncé
« si tout le monde aime les chats, alors quelqu'un aime les chats » est la suivante :
(∀x)Fx → (∃x)Fx.
Si l'on écrit (en fait, dans l'esprit du 2e ordre) :
(∀F)[(∀x)Fx → (∃x)Fx]
alors pour Quine, « (∀F) » ne peut pas être interprété
comme « chaque terme général F est tel que » car, je cite :
|
« Pouvons-nous adopter pour '(∀F)' la lecture 'chaque terme général (ou prédicat)
F est tel que', et pour '(∃F)' une lecture correspondante ?
Non, car ceci serait une confusion. 'F ' n'a jamais été conçu comme référant à des
termes généraux (et donc comme tenant la place de noms de termes généraux), mais seulement
comme tenant la place de termes généraux. S'il existait des objets d'un type spécial,
mettons des garigous, dont des termes généraux seraient les noms, alors les lectures correctes
de '(∀F)' et '(∃F)' seraient 'chaque garigou F est tel que'
et 'quelque garigou F est tel que'. Mais la difficulté est que les termes généraux
ne sont aucunement des noms. »
|
Si l'on veut que « F » prenne le statut de variable — ce qui revient
à procéder à un
détournement de son usage habituel — Quine propose alors d'utiliser des classes pour le parcours
de cette variable. Je cite :
|
« Nous pouvons lire '(∀F)' et '(∃F)' respectivement 'chaque classe
F est telle que' et 'quelque classe F est telle que', à condition simplement
que pour les besoins de la cause nous relisions aussi ' Fx ' comme 'x est un membre
de la classe F '. »
|
Pour éviter toute confusion, Quine propose de substituer à l'utilisation du terme général
« F » celle d'un nom de classe, par exemple « α ».
Ainsi, au lieu de
« (∀F)[(∀x)Fx → (∃x)Fx] »,
on écrira
« (∀α)[(∀x)(x ∈ α) →
(∃x)(x ∈ α)] ».
Pour chaque objet x appartenant à la classe α, la variable « x »
parcourt ici un certain univers U et la variable « α » un univers
différent U1, dont chaque objet est une classe, à savoir une certaine propriété partagée
par les objets de U.
Mais à propos du schéma :
(∀α)[(∀x)(x ∈ α) →
(∃x)(x ∈ α)]
on ne voit pas quelle en serait la valeur ajoutée par rapport au tout premier
« (∀x)Fx → (∃x)Fx ».
Quine exprime la chose ainsi :
|
« Si tous les énoncés formulables dans notre notation pour la théorie des classes pouvaient
ainsi être ramenés à des expressions consistantes et valides de la théorie de la quantification,
nous pourrions regarder notre théorie des classes comme une simple transcription pittoresque
de notre théorie de la quantification, les classes n'auraient nul besoin d'être reconnues
comme des entités sérieusement présupposées. »
|
Jusqu'ici, on pouvait donc se limiter aux termes généraux de la logique du 1er ordre et s'abstenir
d'en passer par des classes. Par contre, Quine précise que la théorie des classes devient nécessaire,
quand parmi les quantificateurs prénexes (c'est-à-dire quand les quantificateurs ont tous été
regroupés en tête d'une formule quantifiée) figurent à la fois des quantificateurs universels
et existentiels. Par exemple :
(∀α)(∃β)(∀x)
[(x ∈ α) ←→ (x ∈ β)]
(∀x)(∀y)(∃α)
[(x ∈ α) ←→ (y ∈ α)]
On débouche en fait dans un système qui cette fois-ci est hors de portée de la logique du premier ordre.
Quine donne deux exemples nécessitant l'utilisation des classes. Par exemple, celui de la généalogie :
« x est un ancêtre de y » (la récursivité montre le bout de son nez...),
ou celui des gens qui s'admirent mutuellement (certaines personnes s'admirent l'une l'autre et
n'en admirent aucune autre). A partir de l'exemple des ancêtres, on déboule en fait tout droit
dans la théorie générale des classes, ou théorie des ensembles. La construction utilisée dans
la définition du terme ancêtre fut utilisée par Frege (1879) pour être appliquée aux nombres,
considérés comme classes de classes.
Il est légitime de penser que, dans le cadre du Modèle Relationnel de Données, il n'est pas nécessaire
d'en arriver là. De fait, en 1970, Codd en est revenu à la logique du 1er ordre. S'il en était resté à
son énoncé de 1969, il est vraisemblable que le Modèle Relationnel de Données aurait intéressé les
chercheurs, mais n'aurait pas connu le succès qui fut le sien⁽¹⁾,
et le plus célèbre de ses avatars, le modèle SQL, n'aurait pas vu le jour. Pour nos bases de données,
à moins que les SGBD à Orientation Objet aient réussi à s'imposer, nous continuerions à exploiter
essentiellement des systèmes hiérarchiques, listes inverses ou CODASYL. Pour avoir les avoir beaucoup
fréquentés, j'en ai les jambes qui flageolent...
C.5. L'exemple de la généalogie et ses applications
Pour mieux percevoir la nécessité dans certaines circonstances d'utiliser des classes,
on peut se pencher sur le cas de la généalogie proposé par Frege. Quine présente ainsi
la chose, je cite :
|
« Comprenons 'ancêtre' dans un sens légèrement élargi, en comptant comme les ancêtres
d'une personne non seulement ses parents, ses grands-parents, et ainsi de suite, mais aussi
cette personne elle-même. Représentons 'parent' par ' F ', de façon que ' Fxy '
signifie ' x est parent de y '. [...]
Un trait important de la classe des ancêtres de ' y ' est que tous les parents de membres
de la classe en sont membres à leur tour. Un autre de ses traits est que y lui-même en fait
partie. Mais ces deux traits ne déterminent pas encore la classe des ancêtres de y de façon unique,
il existe des classes plus vastes qui contiennent à la fois y et tous les parents de leurs
membres. Une classe de ce type est la classe des ancêtres des petits-fils de y. Un autre
exemple est la classe combinée des ancêtres de y et des cravates ; car les cravates étant
sans parents, leur inclusion ne change rien au fait que tous les parents des membres sont
des membres. Il est clair, en revanche, que toute classe qui contient y et tous les parents
de ses membres devra au moins contenir tous les ancêtres de y, quelles que soient les autres
choses qu'il puisse lui arriver de contenir. En outre, l'une de ces classes contient exclusivement
les ancêtres de y. D'où la conséquence que pour être un ancêtre de y il est
nécessaire et suffisant d'appartenir à toute classe contenant y et tous les parents de
ses membres. En conséquence ' x est un ancêtre de y ' pourra s'écrire ainsi :
x appartient à toute classe contenant y et tous les parents de ses membres ;
C'est-à-dire :
(∀α) [(y ∈ α)
. (tous les parents des membres de α
appartiennent à α) → (x ∈ α)] ;
et donc :
(∀α) [(y ∈ α) .
(∀z)(∀w) [(w ∈ α)
. Fzw . → (z ∈ α)]
→ (x ∈ α)}.
Cette construction ingénieuse est susceptible de nombreuses applications hors de la généalogie. [...]
Mais l'aspect significatif de cette construction pour notre présente démarche est qu'elle fait un
usage essentiel de la quantification d'une variable de classe 'α'. »
|
L'avant-dernier énoncé fourni par Quine peut être ainsi paraphrasé :
|
Quelle que soit la classe α, si y appartient à cette classe et si tous
les parents des membres de cette classe en font aussi partie, alors le parent x
de y appartient lui aussi à cette classe.
|
Dans le dernier énoncé, bien que cela ne soit pas strictement nécessaire, Quine procède à un
changement de variables (apparition des variables w et z), sans doute pour mettre
en évidence le fait que x et y sont libres d'un côté et liées quand elles sont
utilisées avec des quantificateurs.
Dans la foulée, et toujours en se référant à Frege, Quine propose a son tour la formule qui
sous-tend l'induction mathématique (« Nx » se lit « x est un nombre ») :
Nx ←→ (∀α)
{(0 ∈ α) . (∀z)
[(z ∈ α) → (1+z ∈ α)]
→ (x ∈ α)}
C'est-à-dire : Pour toute classe α, si 0 appartient à α et si
la proposition « si tout nombre z appartient à α alors son successeur
appartient aussi à α » alors tout nombre appartient à α.
Autrement dit, être un nombre c'est appartenir à chaque classe à laquelle appartient 0 ainsi que
le successeur de chaque membre de la classe.
C.6. Au sujet des RVA de Date et Darwen
Au paragraphe 2.6, on a vu que pour Date et Darwen, un attribut peut prendre une relation pour valeur,
à condition de respecter la 1NF pour laquelle est mieux cerné le principe de l'atomicité
(cf. paragraphe 2.7) : dans chaque tuple, chaque attribut contient exactement une valeur
(groupes répétitifs interdits).
Il n'y a pas a priori de problème de dérive vers la logique du deuxième ordre, car les opérateurs
relationnels déjà en place suffisent : si on a besoin de manipuler des données emboîtées, telles
que les livraisons de pièces (cf. « Inconvénients des RVA » au paragraphe 2.6), on utilise
à cet effet le couple d'opérateurs GROUP/UNGROUP, lesquels ne sont jamais que des combinaisons
d'opérateurs existants, des raccourcis, du « syntactic sugar ». Appliquée aux RVA,
la formulation de requêtes du genre : « Quels fournisseurs ont livré quelles pièces ? »,
« Quelles pièces ont été livrées par quels fournisseurs ? », etc.
ne pose aucun problème.
Il faudrait passer à une logique du 2e ordre si l'on était confronté à des problèmes comparables
à ceux posés par A. Tarski. Je cite Gianbruno Guerrerio dans Gödel : logique à la folie
(Pour la science, numéro 20) :
|
« La distinction entre axiomes du 1er ordre et du 2e ordre a été établie par le logicien polonais
Alfred Tarski pour distinguer le langage-objet d'une étude, c'est-à-dire le langage utilisé pour parler
d'objets quelconques, du métalangage correspondant, c'est-à-dire du langage utilisé pour parler
du langage objet. Il existe même un méta-métalangage qui parle du métalangage, etc. »
|
Tarski a prouvé qu'à défaut, on tomberait dans le paradoxe du menteur (« Je mens »).
3lignes.jpg) |
Cela dit, les RVA ne contiennent que des valeurs (relations), jamais de variables (relvars),
et les logiciens que Date a consultés n'ont pas pu montrer que l'utilisation des RVA nécessitait d'en
passer par une logique du 2e ordre.
|
_______________________________________
(1)
Certains ont trouvé le Modèle relationnel trop simple et ont proposé de le remplacer par des modèles
plus « puissants », mais qui en fait sont confinés dans des niches limitées à des sujets particuliers.
D. La normalisation et le bonhomme NULL
Dans les énoncés des formes normales, il n'est pas fait mention des effets que peut produire la présence
du bonhomme NULL dans les dépendances. Il n'est pas inutile de connaître quelques unes des réflexions de
Codd et Date à ce sujet. On peut aussi consulter les ouvrages ou communications de chercheurs et auteurs
tels que Yannis Vassiliou ou David Maier [Maier 1983]. Rappelons que ce que Codd appelle
une A-mark est une marque (ou un marqueur) « applicable », dont on se sert quand une valeur est inconnue,
marque qui peut être remplacée par une valeur réelle à tout moment (cas par exemple du numéro de SIRET
de telle entreprise, numéro provisoirement inconnu). Une I-mark est une marque (ou un marqueur)
« inapplicable » quand il n'y a pertinemment pas de valeur à fournir (cas par exemple du nom marital pour
les salariés du sexe masculin).
Concernant Codd
Voici ce que l'on peut lire dans [Codd 1990] au paragraphe 8.21 « Normalization »,
page 193, traduisons :
|
Les concepts de dépendance fonctionnelle, multivaluée et de jointure, ainsi que les règles régissant
celles-ci ont été développés sans que soient mentionnés les problèmes pouvant résulter de
l'absence de valeurs.
Les formes normales basées sur ces dépendances ont été développées sans tenir compte non plus de l'absence
éventuelle de valeurs. Est-ce que la possibilité de la présence de marques dans certaines colonnes
(chaque marque signalant l'absence de valeur) peut saper l'ensemble de ces concepts et des théorèmes
qui les utilisent ? Heureusement, la réponse est non : une marque n'est pas une valeur. Plus précisément,
une marque dans une colonne C est sémantiquement différente d'une valeur dans C. Ainsi, d'une manière générale,
les concepts utilisés dans la normalisation ne s'appliquent pas et ne devraient pas s'appliquer aux
combinaisons de lignes et de colonnes contenant des marques. En revanche :
|
indente.jpg) |
Les concepts de la normalisation devraient être utilisés au stade de la version conceptuelle de la base
de données, auquel cas les lignes contenant des informations du type absent-mais-applicable
dans les colonnes concernées ne sont pas à prendre en compte ;
|
indente.jpg) |
Ces concepts devraient en outre s'appliquer quand on cherche à remplacer une marque par une valeur.
|
|
Lors d'une tentative d'insertion d'une ligne dans une relation, si une valeur est absente,
il est sans objet pour le système de chercher à accepter ou rejeter cette ligne sur la base du respect
ou du non respect des contraintes d'intégrité liées à une dépendance auxquelles est soumise telle ou
telle colonne. Ce n'est que lorsqu'on cherche à remplacer une marque par une valeur que le système
doit prendre les mesures qui s'imposent, en fonction de ces contraintes.
On pourrait être tenté de traiter les I-marks de façon différente des A-marks. Cependant,
certains utilisateurs peuvent être autorisés à remplacer une I-mark par une valeur. Toutes ces marques
doivent être traitées de la même façon, quel que soit leur type, en matière de test de contrainte de
dépendance, que cette dernière soit fonctionnelle, multivaluée, de jointure ou d'inclusion. Pour chaque
ligne contenant une marque dans les colonnes impliquées, le SGBD ne devrait réagir que lorsqu'une tentative
est faite de remplacer par une valeur réelle des éléments qui sont marqués.
|
Quand Codd écrit :
|
Les concepts de la normalisation devraient être utilisés au stade de la version conceptuelle
de la base de données...
|
on peut penser qu'il s'adresse à ceux qui conçoivent des diagrammes du type Entité/Relation. Quoi qu'il
en soit, les concepteurs doivent effectivement être compétents en ce qui concerne la normalisation, ou à
tout le moins pratiquer la double approche descendante/ascendante et ne jamais autoriser
la présence du bonhomme NULL.
Codd poursuit (page 200 du même ouvrage), manifestement à l'attention de Date :
|
Les détracteurs semblent avoir rejeté, sans en fournir la raison, une troisième option qui est celle
adoptée par le Modèle Relationnel. C'est-à-dire qu'à chaque fois que le composant A d'une ligne est manquant
(ou le devient), le SGBD n'a pas à vérifier la dépendance fonctionnelle A ➔ B,
tant qu'une tentative de remplacement de la marque (null) dans la colonne A par une valeur réelle n'a pas
eu lieu.
L'exemple suivant a pour objet d'illustrer l'absence d'effet des valeurs absentes sur la normalisation.
La relation EMP identifie et décrit les employés. Trois de ses colonnes sont présentées :
E# : Numéro de l'employé (clé primaire)
D# : Numéro du département
CT : Type de contrat
Dans l'entreprise, à un département on affecte exactement un type de contrat. On fera référence
à cette contrainte en l'appelant Règle 1. Une conséquence de cette règle est que la relation EMP
n'est pas en troisième forme normale. Il existe les dépendances fonctionnelles suivantes :
E# ➔ D# ➔ CT
Il est à noter que le département D# auquel est affecté l'employé E# est une propriété
immédiate de l'employé, tandis que le type de contrat CT est une propriété immédiate du
département. Dans la colonne CT, figurent les valeurs g et n. Elles dénotent deux types
de contrats, respectivement passés avec l'État ou non.
|
.jpg)
|
Dans cet exemple, les deux numéros manquants doivent être distincts, en vertu de la règle 1 et
aussi parce que les types de contrats dans les deux lignes concernées sont différents.
Les problèmes liés au contrôle des dépendances fonctionnelles quand il y a des valeurs absentes
peuvent être totalement évités en différant le contrôle de conformité de chaque ligne avec la
dépendance fonctionnelle D# ➔ CT jusqu'à ce que se produise une tentative
de remplacement d'un numéro de département absent par une valeur réelle.
|
3lignes.jpg) |
Quoi qu'il en soit, le piège s'est refermé, on ne peut plus normaliser EMP :
le théorème de Heath n'est plus applicable,
intégrité d'entité oblige (cf. paragraphe 3.2.6).
Comme le reconnaît Codd, la décomposition aurait dû avoir lieu dès
le niveau conceptuel (MCD Merise, diagramme de classes...)
|
Concernant Date
Le « détracteur » avait déjà attiré notre attention sur le point
que nous venons d'évoquer. Il présente un schéma fort
intéressant, à la page 219 de [Date 1985] paragraphe 5.5 « Null values », et là encore le théorème
de Heath est mis en échec, traduisons :
|
Si la relation R (A, B, C) satisfait à la dépendance fonctionnelle A ➔ B,
alors R peut être décomposée sans perte [de contenu] selon ses
projections R1 (A, B) et R2 (A, C),
c'est-à-dire que l'on peut retrouver R par la jointure naturelle de R1 et de R2
sur A. Il est facile de vérifier que [ce] théorème ne tient plus si A
peut prendre des valeurs nulles. Par exemple, si R est ainsi représentée :
|
|
alors les projections R1 et R2 ainsi que leur jointure naturelle sont les suivantes :
|
=> Une fois de plus, anticipons au niveau conceptuel.
E. Fermeture des dépendances fonctionnelles, axiomes d'Armstrong, ensemble irréductible
E.1. Fermeture d'un ensemble de dépendances fonctionnelles
Avant de démontrer qu'une relvar R est en forme normale de Boyce-Codd (BCNF), il faut en passer par une
tâche (théoriquement) incontournable (et prodigieusement ennuyeuse...), à savoir produire l'ensemble des
dépendances fonctionnelles (DF) vérifiées par R. Pour cela nous disposons initialement
de l'ensemble S des DF vérifiées
par R, issues directement des règles de gestion des données de l'entreprise, et nous complétons cet
ensemble en y ajoutant toutes les DF que l'on peut en inférer grâce à un système de règles, connues sous
le nom d'axiomes d'Armstrong.
L'ensemble que nous obtenons au final est appelé fermeture (closure) de S, noté S+.
L'exercice consistant à calculer la fermeture en jonglant avec ces règles se révèle être
rarement trivial.
Chris Date décrit avec humour la méthode à employer : « Appliquez
ces règles de façon répétitive,
jusqu'à ce qu'elles ne produisent plus de nouvelles DF... »,
ce qui peut laisser sous-entendre que, plus le nombre d'attributs impliqués est élevé,
ainsi que celui des DF, plus la recherche peut être longue et décourageante, autrement dit,
calculer S+ est incomparablement plus facile à dire qu'à faire, et l'exercice qui suit
(cf. paragraphe E.3)
en donne un avant-goût (fermeture de près de 30 éléments pour seulement trois attributs et deux DF...)
On peut aussi s'exercer avec l'exemple proposé par Jeff Ullman (au départ, six attributs
et 8 DF,
cf. paragraphe E.5.1). Quoi qu'il en soit...
E.2. Axiomes d'Armstrong
Soit A, B, C, D des sous-ensembles quelconques d'attributs d'une relvar donnée R et notons AB
l'union de A et de B. Les règles permettant de produire de nouvelles DF à partir d'un ensemble
donné de DF sont les suivantes, et sont connues sous le nom d'axiomes d'Armstrong [Armstrong 1974],
déjà formulés par Delobel et Casey [Delobel 1973],
axiomes complets et valides [Ullman 1982] :
1.
Réflexivité : si B est un sous-ensemble (non nécessairement strict) de A,
alors A ➔ B.
2.
Augmentation : si A ➔ B, alors AC ➔ BC
3.
Transitivité : si A ➔ B et B ➔ C alors A ➔ C
|
-
Ces axiomes sont complets en ce sens qu'ils permettent,
à partir d'un ensemble donné S de DF vérifiées par R,
de produire toutes les DF pouvant en être inférées, c'est-à-dire la fermeture S+ de S.
-
Ces axiomes sont valides car ils ne produisent pas de DF parasites, c'est-à-dire non
impliquées par S.
Des règles fort utiles peuvent être inférées des axiomes :
4.
Décomposition : si A ➔ BC, alors A ➔ B et A ➔ C
5.
Union : si A ➔ B et A ➔ C, alors A ➔ BC
6.
Pseudo-transitivité : si A ➔ B et BC ➔ D alors AC ➔ D
7.
Composition : si A ➔ B et C ➔ D alors AC ➔ BD
|
A titre d'exemple, la règle de décomposition peut être établie ainsi :
|
1. A ➔ BC
|
(donné)
|
|
2. BC ➔ B
|
(réflexivité)
|
|
3. A ➔ B
|
(1, 2 et transitivité)
|
|
4. BC ➔ C
|
(réflexivité)
|
|
5. A ➔ C
|
(1, 4 et transitivité)
|
De même, pour la règle de composition :
|
1. A ➔ B
|
(donné)
|
|
2. AC ➔ BC
|
(augmentation)
|
|
3. C ➔ D
|
(donné)
|
|
4. BC ➔ BD
|
(augmentation)
|
|
5. AC ➔ BD
|
(2, 4 et transitivité)
|
Ou encore, pour la règle de pseudo-transitivité :
|
1. A ➔ B
|
(donné)
|
|
2. AC ➔ BC
|
(augmentation)
|
|
3. BC ➔ D
|
(donné)
|
|
4. AC ➔ D
|
(2, 3 et transitivité)
|
E.3. Application des axiomes, calcul de la fermeture des DF
Concernant la recherche pour une relvar R de la fermeture S+ à partir d'un ensemble S de DF,
on se convainc rapidement que la tâche est de longue haleine. A titre d'exercice, prenons le
cas de la bien modeste
relvar EMP, utilisée pour décrire l'enseignement des matières à des étudiants par des professeurs, et
qui ne contient que trois attributs (cf. paragraphe 3.7). Remplaçons les noms des
attributs Etudiant, Matiere et Professeur respectivement par E, M et P.
L'ensemble donné S des DF est le suivant :
a) Indépendamment de l'ensemble S, par application de l'axiome de réflexivité,
on produit les DF triviales :
|
DF01 : {E,M,P} ➔ {E,M,P}
DF02 : {E,M,P} ➔ {E,M}
DF03 : {E,M,P} ➔ {E,P}
DF04 : {E,M,P} ➔ {M,P}
DF05 : {E,M,P} ➔ {E}
DF06 : {E,M,P} ➔ {M}
DF07 : {E,M,P} ➔ {P}
DF08 : {E,M} ➔ {E,M}
DF09 : {E,M} ➔ {E}
DF10 : {E,M} ➔ {M}
DF11 : {E,P} ➔ {E,P}
DF12 : {E,P} ➔ {E}
DF13 : {E,P} ➔ {P}
DF14 : {M,P} ➔ {M,P}
DF15 : {M,P} ➔ {M}
DF16 : {M,P} ➔ {P}
DF17 : {E} ➔ {E}
DF18 : {M} ➔ {M}
DF19 : {P} ➔ {P}
|
b) Les deux DF non triviales qui suivent composent S,
elles appartiennent donc à S+ :
|
DF20 : {E,M} ➔ {P}
DF21 : {P} ➔ {M}
|
c) Par application de l'axiome d'augmentation à DF20, on produit les DF suivantes :
|
DF22 : {E,M} ➔{E,P}
(augmentation par E)
DF23 : {E,M} ➔ {M,P}
(augmentation par M)
DF24 : {E,M} ➔ {E,M,P}
(augmentation par E et M)
|
d) Par application du même axiome à DF21, on produit les DF suivantes :
|
DF25 : {P} ➔ {M,P}
(augmentation par P)
DF26 : {E,P} ➔ {E,M}
(augmentation par E)
DF27 : {E,P} ➔ {E,M,P}
(augmentation par E et P)
|
e) Par application de l'axiome de transitivité à DF13 et DF21, on produit la DF suivante :
f) Par application de l'axiome de transitivité à DF26 et DF23, on produit la DF suivante :
Ainsi, grâce aux seuls axiomes (réflexivité, augmentation, transitivité), on est à même de calculer
la fermeture S+.
Pour en revenir au problème initial, à savoir prouver qu'une relvar R est en BCNF, on sait qu'il suffit
que le déterminant de chaque DF non triviale vérifiée par R en soit une surclé
(ou encore que le déterminant de chaque DF irréductible à gauche soit une clé candidate).
Il était donc probablement inutile de fournir ici la
(longue) liste des DF triviales, mais celles-ci pouvaient être utiles, à l'instar de DF13
qui a été impliquée dans la production de DF28. Bien sûr, on aurait pu obtenir ce résultat
en appliquant, par exemple, à DF26 la règle de décomposition (mais celle-ci est inférée
de l'axiome de réflexivité). Tous les coups sont bons. Quoi qu'il en soit, on peut désormais
se concentrer sur l'ensemble des DF non triviales :
|
DF20 : {E,M} ➔ {P}
DF22 : {E,M} ➔ {E,P}
DF23 : {E,M} ➔ {M,P}
DF24 : {E,M} ➔ {E,M,P}
DF21 : {P} ➔ {M}
DF25 : {P} ➔ {M,P}
DF28 : {E,P} ➔ {M}
DF26 : {E,P} ➔ {E,M}
DF27 : {E,P} ➔ {E,M,P}
DF29 : {E,P} ➔ {M,P}
|
Dans ce sous-ensemble, on repère facilement les surclés (donc les clés candidates) de la relvar EMP.
D'après DF24 et DF27, il s'agit de {E,M} et {E,P},
car les dépendants de ces DF ont pour éléments tous les attributs de l'en-tête de EMP.
Par ailleurs, on voit tout de suite que la BCNF est violée car, par exemple,
le déterminant {P} de la
DF DF21 n'est pas surclé. Certes on le savait dès le départ,
mais pour autant, dans le cas général,
en l'absence de S+ — ou si l'on n'est pas certain de sa complétude
— d'éventuelles DF fautives
peuvent passer au travers des mailles du filet, auquel cas on ne peut pas
jurer de la normalité
d'une relvar.
Toutefois, sachons qu'il est possible de s'assurer du respect de la BCNF
tout en faisant l'impasse sur S+. En se basant seulement sur S,
on peut adopter une
stratégie moins coûteuse en temps de calcul, plus sûre et
plus efficace, grâce à l'algorithme précieux
et incontournable qui suit.
E.4. Fermeture d'un ensemble d'attributs, l'algorithme du seau à dépendants
Comme on vient de le voir, calculer la fermeture S+ d'un ensemble S de DF vérifiées
par une relvar R peut très rapidement s'avérer mission impossible, lorsque le nombre
d'attributs de l'en-tête de R croît, ainsi que le nombre de DF qu'elle vérifie.
Heureusement, étant donnés un sous-ensemble Z des attributs de l'en-tête
de R et l'ensemble S des DF vérifiées par R,
on dispose d'un algorithme (conçu par Philip Bernstein [Bernstein 1976]),
permettant de déterminer de façon très simple
l'ensemble des attributs de R dépendant fonctionnellement de Z,
ce que l'on appelle la fermeture Z+ de Z
par rapport à S.
Sans avoir à en passer par les axiomes d'Armstrong, on pourra de façon mécanique,
confirmer ou infirmer l'existence d'une hypothétique
DF X ➔ Y,
selon qu'au résultat cette DF appartient ou non à la fermeture X+ de X par rapport S.
Et, cerise sur le gâteau,
si Y contient l'ensemble
des attributs de l'en-tête de R, alors (par référence à la définition de la surclé) X
est surclé.
L'algorithme en question permet donc de trouver l'ensemble des attributs qui sont
fonctionnellement dépendants de Z.
Le résultat est fourni dans une variable, appelons-la V. La méthode est la suivante
(voir par exemple [Date 2004], paragraphe 11.5, [Maier 1983], « Algorithm 4.2 »,
[Ullman 1982], « Algorithm 7.1 », « Theorem 7.2 » pour
en démontrer la validité) :
V := Z ;
Repeat
For each dépendance fonctionnelle X ➔ Y appartenant à S
Do
Begin
If X
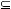 V V
Then V := V
 Y Y
End
Until V n'a pas changé au cours de l'itération
|
Illustrons à l'aide d'un exemple utilisé par Chris Date.
La relvar R est composée des attributs A, B, C, D, E, F.
L'ensemble S de DF donné est le suivant :
{A} ➔ {B,C}
{E} ➔ {C,F}
{B} ➔ {E}
{C,D} ➔ {E,F}
|
Calculons par exemple la fermeture {A,B}+ de {A,B} par rapport à S :
-
On initialise la variable V avec la valeur "{A,B}". De façon imagée, V est
comme un
seau dans lequel on
jette la paire {A,B}. Le but est d'amorcer la pompe qui servira ensuite
à y aspirer un maximum
d'attributs de l'en-tête de R, lesquels pourront ainsi constituer
un dépendant pour une DF ayant {A,B} comme déterminant.
Cet amorçage met systématiquement à profit l'axiome de réflexivité,
laquelle nous permet
d'affirmer que {A,B} ➔ {A,B} donc,
avec une pelle à dépendants,
ramasser le dépendant de cette DF, c'est-à-dire la paire {A,B} et
la jeter dans le seau.
Pour le moment, on sait simplement que {A,B} ➔ {A,B}, ce qui est trivial,
mais il faut un début à tout.
-
Suite des opérations :
Pour la première DF, {A} ➔ {B,C}, parce que le
déterminant {A} est déjà dans le seau,
on peut y jeter à son tour le dépendant {B,C}.
Par union avec {A,B}, le seau contient
maintenant {A,B,C}. Cette capture est valide du fait que :
 {A,B} ➔ {A} (réflexivité) ;
{A,B} ➔ {A} (réflexivité) ;
 La DF {A} ➔ {B,C} est donnée, donc par transitivité on produit la DF
{A,B} ➔ {B,C} ;
La DF {A} ➔ {B,C} est donnée, donc par transitivité on produit la DF
{A,B} ➔ {B,C} ;
 Et par augmentation : {A,B} ➔ {A,B,C}.
Et par augmentation : {A,B} ➔ {A,B,C}.
On sait maintenant que {A,B} ➔ {A,B,C}, ce qui n'est pas forcément trivial
à montrer sans l'algorithme.
-
Pour la DF suivante {E} ➔ {C,F}, le déterminant {E}
n'étant pas dans le seau, on ne peut pas y jeter C et F.
-
{A,B,C} constitue le contenu actuel du seau.
Pour la DF suivante {B} ➔ {E}, le
déterminant {B} étant dans le seau en tant que sous-ensemble de {A,B,C},
on peut y jeter le dépendant {E}. Le seau contient maintenant
{A,B,C,E}. La validité
de la capture met encore en jeu l'enchaînement réflexivité, transitivité,
augmentation :
 {A,B,C} ➔ {B} (réflexivité) ;
{A,B,C} ➔ {B} (réflexivité) ;
 La DF {B} ➔ {E} est donnée, donc par transitivité on produit la DF
{A,B,C} ➔ {E} ;
La DF {B} ➔ {E} est donnée, donc par transitivité on produit la DF
{A,B,C} ➔ {E} ;
 Et par augmentation, {A,B,C} ➔ {A,B,C,E}.
Et par augmentation, {A,B,C} ➔ {A,B,C,E}.
-
Pour la DF suivante {C,D} ➔ {E,F},
comme {C,D} n'est pas un sous-ensemble de {A,B,C,E}, on ne peut que passer à la suite.
-
Chaque DF a été examinée et l'on repart pour un tour de manège.
A la première itération, le contenu du seau ne change pas.
A la deuxième itération, du fait que le déterminant {E} de la DF
{E} ➔ {C,F}
est cette fois-ci dans le seau, toujours en enchaînant réflexivité,
transitivité et augmentation,
on peut y jeter {C,F}. Le contenu du seau devient {A,B,C,E,F}.
Les troisième et quatrième itérations laissent le contenu du seau inchangé.
-
On repart pour un tour de manège complet, lequel n'apporte rien de nouveau :
le traitement est terminé avec un seau ayant pour contenu {A,B,C,E,F}.
On a prouvé que {A,B} ➔ {A,B,C,E,F} et qu'on ne peut pas faire
mieux avec le déterminant {A,B}.
Ce qui est sûr et constitue une information précieuse, c'est qu'à partir
de l'ensemble S des DF
qui ont été données, {A,B} ne
peut pas constituer une surclé (a fortiori une clé candidate),
car en fin de parcours
le seau ne contient pas tous les attributs de R :
l'attribut D manque en effet à l'appel.
Grâce à l'algorithme, on peut aussi montrer que {A} ➔ {A,B,C,E,F},
c'est-à-dire que {A}+ = {A,B}+ par rapport à S.
Méthode pratique
Pour ne pas perdre de temps on peut procéder de façon pragmatique. Prenons par exemple
le cas de {A}+ :
Prévoir dans le seau une place pour chaque attribut de la relvar R et amorcer la pompe
à partir de la DF triviale {A} ➔ {A}. Le contenu du seau ressemble à ceci :
A _ _ _ _ _
Capturer les attributs B et C parce que l'attribut A est dans le seau et qu'il existe la DF
{A} ➔ {B,C} :
A B C _ _ _
Capturer l'attribut E parce que l'attribut B est dans le seau et qu'il
existe la DF {B} ➔ {E} :
A B C _ E _
Capturer l'attribut F parce que l'attribut E est dans le seau et qu'il
existe la DF {E} ➔ {C,F} :
A B C _ E F
En revanche, rien ne permet de capturer l'attribut D :
fin des opérations concernant {A}+.
Autre exemple. On montre sans difficulté que {A,D} est une surclé de la relvar R en
procédant ainsi :
Amorcer la pompe :
A _ _ D _ _
Capturer les attributs B et C parce que l'attribut A est dans le seau et qu'il existe
la DF {A} ➔ {B,C} :
A B C D _ _
Capturer les attributs E et F parce que les attributs C et D sont dans le seau et qu'il existe
la DF {C,D} ➔ {E,F} :
A B C D E F
Autrement dit, {A,D} ➔ {A,B,C,D,E,F} et {A,D}
est une surclé pour R
(et c'est aussi une clé candidate, car {A,D}+ est différent
de {A}+ et {D}+).
Par comparaison, on se convaincra facilement que sans l'algorithme,
parvenir à ce résultat
demande beaucoup plus de réflexion.
Par exemple :
|
1. {A,D} ➔ {A}
|
(réflexivité)
|
|
2. {A} ➔ {B,C}
|
(donné)
|
|
3. {A,D} ➔ {B,C,D}
|
(2, augmentation)
|
|
4. {A,D} ➔ {A,B,C,D}
|
(3, augmentation)
|
|
5. {A} ➔ {B}
|
(2, décomposition)
|
|
6. {B} ➔ {E}
|
(donné)
|
|
7. {A} ➔ {E}
|
(5, 6, transitivité)
|
|
8. {A,D} ➔ {D,E}
|
(7, augmentation)
|
|
9. {A,D} ➔ {A,B,C,D,E}
|
(4, 8, union)
|
|
10. {E} ➔ {C,F}
|
(donné)
|
|
11. {B} ➔ {C,F}
|
(6, 10, transitivité)
|
|
12. {A} ➔ {C,F}
|
(5, 11, transitivité)
|
|
13. {A,D} ➔ {C,D,F}
|
(12, augmentation)
|
|
14. {A,D} ➔ {A,B,C,D,E,F}
|
(9, 13, union)
|
Supposons encore que l'on ait l'intuition que la DF {C,D} ➔ {F}
puisse être inférée d'autres DF et donc être évacuée de l'ensemble S
de DF proposé ci-dessus,
lequel se réduirait par conséquent à T :
{A} ➔ {B,C}
{E} ➔ {C,F}
{B} ➔ {E}
{C,D} ➔ {E}
|
On montre qu'il en est ainsi, à partir de la fermeture {CD}+
par rapport à T.
Au départ, le seau contient les attributs C et D :
_ _ C D _ _
L'attribut E peut être capturé parce que les attributs C et D sont dans le seau et qu'il existe la DF
{C,D} ➔ {E}, obtenue en appliquant la règle de décomposition à la
DF {C,D} ➔ {E,F} :
_ _ C D E _
L'attribut F peut être capturé parce que l'attribut E est dans le seau et qu'il existe la DF
{E} ➔ {C,F} :
_ _ C D E F
En conséquence, {C,D} ➔ {C,D,E,F}. On applique alors la règle de décomposition,
et l'on confirme ainsi que {C,D} ➔ {F}.
La réduction du nombre de DF fait l'objet de la recherche par algorithme des ensembles irréductibles de DF
(cf. paragraphe E.6).
N.B.
Pour en revenir à l'exemple de la relvar EMP (cf. paragraphe E.3), la technique du seau permet
de découvrir facilement quelque chose qui n'est pas forcément intuitif, à savoir que
{E,P} en est une clé candidate (donc une surclé).
E.5. Inventaire des clés et surclés. Quelques observations.
E.5.1. La technique du rouleau compresseur
A l'aide de l'algorithme du seau on vérifie rapidement si au sein de l'ensemble S
des DF associé à une relvar R, il en est qui provoquent un viol de BCNF.
Partons d'un exemple proposé par Jeff Ullman (cf. [Ullman 1982], « Computing closures »),
dans lequel l'ensemble S des DF d'une relvar U {A, B, C, D, E, G}
est le suivant :
DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 : {A,C,D} ➔ {B}
DF05 : {D} ➔ {E,G}
DF06 : {B,E} ➔ {C}
DF07 : {C,G} ➔ {B,D}
DF08 : {C,E} ➔ {A,G}
|
On met très vite en évidence le fait que DF02 et DF05 sont fautives car, contrairement
aux autres DF, la fermeture de leur déterminant n'est pas égale à {A,B,C,D,E,G}.
On pourrait en rester là et normaliser, mais on peut aussi pousser la curiosité jusqu'à dresser
l'inventaire complet des surclés de U
(en fait, la connaissance de ses clés candidates suffit, puisque par
augmentation/décomposition chaque surclé est inférée d'une clé candidate).
Toujours
à l'aide de l'algorithme du seau et en passant en revue les fermetures,
on peut dresser cet inventaire
de façon mécanique,
sans
se poser de questions, pas plus qu'on ne s'en pose avec
un
rouleau compresseur
pour écraser des noix. Roulons donc...
1) On traite par exemple en premier la fermeture par rapport à S de chaque singleton
pour vérifier s'il peut être clé candidate :
{A}, {B}, {C}, {D}, {E}, {G}
et l'on constate très rapidement qu'aucun d'eux ne fait l'objet d'une telle clé :
{A}
50pc.jpg)
{B,C,D,E,G}, etc.
2) On passe ensuite en revue la fermeture par rapport à S de chaque paire :
{A,B}, {A,C}, {A,D}, {A,E}, {A,G}, {B,C}, {B,D}, {B,E}, {B,G}, {C,D}, {C,E}, {C,G}, {D,E}, {D,G}, {E,G}.
Grâce à l'algorithme, du seau, on découvre que 7 de ces 15 paires, à savoir
{A,B}, {B,C}, {B,D}, {B,E}, {C,D}, {C,E}, {C,G}
constituent autant de clés candidates.
Ainsi {A,B}
+ = {A,B,C,D,E,G}, c'est-à-dire {A,B} ➔ {A,B,C,D,E,G}, etc.
3) On passe ensuite en revue la fermeture par rapport à S de chaque triplet
qui ne constitue pas une surclé pouvant être inférée des clés candidates que
l'on vient d'énumérer :
{A,D,E}, {A,D,G}, {A,E,G}, {D,E,G}.
Toujours avec le même algorithme, on montre qu'aucun de ces triplets ne constitue une clé candidate
(donc une surclé).
Le travail est
de facto terminé (et s'il avait fallu poursuivre, on aurait soumis au même régime
les quadruplets, puis les quintuplets, etc.)
Ainsi, on a mis en évidence toutes les clés candidates pour U (soit 7 clés),
sans avoir
à calculer la fermeture S
+.
L'exercice n'était pas inutile,
car au moins sait-on
dresser
l'inventaire
complet des
clés candidates de la relvar,
grâce auquel on peut mener à son terme le travail de normalisation.
E.5.2. Cas des attributs ne figurant pas dans les dépendants des DF
Considérons une relvar R dotée d'un ensemble S de DF non triviales,
dans lequel il existe des attributs qui sont des éléments
de déterminants de ces DF sans être des éléments des dépendants d'autres DF
(n'est donc pas concerné l'exemple du paragraphe E.5.1, dans lequel tous les attributs qui
sont des éléments des déterminants des DF sont aussi des éléments des dépendants d'autres DF).
Si cette situation se présente, on peut accélérer la constitution de la liste
des clés (et surclés) de R.
Reprenons l'exemple fourni par Chris Date (paragraphe E.4).
A l'aide du rouleau compresseur et du seau
à dépendants, on constate rapidement qu'aucun des singletons
{A}, {B}, {C}, {D}, {E}, {F} n'est clé.
Passons aux paires :
{A,B}, {A,C}, {A,D}, {A,E}, {A,F}, {B,C}, {B,D}, {B,E}, {B,F}, {C,D}, {C,E}, {C,F}, {D,E}, {D,F}, {E,F}.
A l'exception de {A,D}, inutile de les soumettre à l'épreuve du seau. On observe en effet que
ni l'attribut A ni l'attribut D ne sont des éléments du dépendant de quelque
DF que ce soit de S, en conséquence de quoi,
l'algorithme ne pourra jamais faire tomber
ces deux attributs dans le seau à partir des paires énumérées autres que {A,D}.
Par exemple, la fermeture {A,B}+ nous permet au mieux de produire {A,B,C,E,F} dont D est
exclu ; même principe pour l'ensemble des paires autres que
{A,D}, la seule finalement qui puisse constituer une clé candidate
(ou participer à une surclé) : soumettre les autres
paires à l'épreuve du seau serait peine perdue.
Pour la même raison, inutile de passer en revue quelque triplet, quadruplet, quintuplet ou
sextuplet que ce soit. En revanche, on peut énumérer les surclés
de R : la paire {A,D et ses sur-ensembles : les triplets {A,B,D}, {A,C,D}, {A,E,D} et {A,F,D},
les quadruplets {A,B,D,E}, {A,B,D,F}, {A,C,D,E}, {A,C,D,F} et {A,D,E,F}, les quintuplets
{A,B,C,D,E}, {A,B,C,D,F} et {A,C,D,E,F}, et enfin le
sextuplet {A,B,C,D,E,F}.
Et l'on peut ainsi dénombrer les infractions concernant
le respect de la BCNF...
En résumé :
3lignes.jpg) |
Si un attribut X d'une relvar R appartient au déterminant d'une DF quelconque de l'ensemble S
des DF (non triviales) vérifiées par R, mais n'appartient à aucun dépendant d'une de
ces DF, alors il participe à chaque clé candidate de R. Reste à chercher les éventuels attributs
en compagnie desquels X pourrait entrer dans la composition d'une clé candidate
(plus généralement d'une surclé),
tâche grandement facilitée par l'utilisation de l'algorithme du seau.
|
E.5.3. Surclés n'ayant pas d'attributs en commun et utilisation de l'algorithme du seau
Attention quand même aux chausse-trapes et aux trous dans le seau.
Reprenons l'exemple fourni par Chris Date (paragraphe E.4).
La relvar R {A,B,C,D,E,F} a pour seule clé la paire {A,D} — ce qui est facile a vérifier
à l'aide de l'algorithme du seau. Mais certains concepteurs ont la manie des clés
(primaires au sens SQL) singletons : à cet effet, ils ajoutent d'office un attribut,
appelons-le K, tel que R a désormais pour en-tête {A,B,C,D,E,F,K} tout en étant dotée cette
fois-ci de deux clés candidates {A,D} et {K}. Attention, dans l'exemple de Chris Date,
l'ensemble S des DF initial est le suivant :
{A} ➔ {B,C}
{E} ➔ {C,F}
{B} ➔ {E}
{C,D} ➔ {E,F}
|
Mais pour tenir compte de K, S doit être aménagé, sinon, en l'état et en utilisant l'algorithme
du seau, il n'y aura toujours qu'une clé pour R, à savoir le triplet {A,D,K}, ce qui n'est pas
franchement le but recherché. Pour que l'algorithme fonctionne, S doit être enrichi en tenant
compte des clés à produire :
{A} ➔ {B,C}
{E} ➔ {C,F}
{B} ➔ {E}
{C,D} ➔ {E,F}
{A,D} ➔ {K}
{K} ➔ {A,D}
|
Ainsi, {K}+ = {A,D}+ = {A,B,C,D,E,F,K}, donc {K} et {A,D} sont bien clés candidates
et le concepteur est satisfait.
E.5.4. Clés oubliées
Bien que son objet premier ne soit pas la production de la fermeture de l'ensemble des DF associées à
une relvar, l'algorithme du seau se révèle indispensable car, comme on l'a vu,
il permet de réduire de façon très simple
et pragmatique le champ de recherche des clés et surclés. Pour reprendre l'exemple du paragraphe E.4
mais en tenant compte des observations faites dans le paragraphe E.5.2, découvrir que la
paire d'attributs {A,D} constitue une clé candidate (donc une surclé) de R n'est pas intuitif
mais se fait de façon naturelle
grâce à l'algorithme et au rouleau compresseur.
Une fois les techniques (quand même simples) maîtrisées,
et les chausse-trapes potentielles
identifiées, la mise en évidence de la liste exhaustive des surclés est généralement rapide.
Il est probable que nombre de bases de données en production contiennent des clés
que l'on n'a malheureusement pas déclarées au SGBD, parce que l'on
n'aura pas cherché à les repérer :
pour chaque table SQL, on se sera contenté de définir une clé primaire (singleton de surcroît),
mais pour le reste...
Quoi qu'il en soit, l'algorithme du seau est au cœur de la méthode utilisée pour
réduire l'ensemble des DF associées à une relvar, sujet traité dans le paragraphe E.6.
E.6. Ensemble irréductible de dépendances fonctionnelles
E.6.1. Ensembles de DF et redondances
Considérons la relvar R {A,B,C,D} dotée de l'ensemble S de DF :
DF01 : {A} ➔ {B}
DF02 : {B,C} ➔ {D}
DF03 : {A,C} ➔ {D}
|
DF03 peut être inférée de DF01 et DF02. En effet :
1 {A} ➔ {B}
(donné)
2 {A,C} ➔ {B,C}
(augmentation)
3 {B,C} ➔ {D}
(donné)
4 {A,C} ➔ {D}
(2, 3 et transitivité)
|
S est donc réductible et peut être remplacé par le sous-ensemble I :
DF01 : {A} ➔ {B}
DF02 : {B,C} ➔ {D}
|
Autrement dit, les fermetures S+ et I+ par rapport à R sont égales.
(Au passage, on aura reconnu la règle de pseudo-transitivité,
qui sert à illustrer
notre propos). L'important dans cette affaire est qu'en remplaçant S par I,
lorsqu'on demandera au SGBD de garantir DF01 et DF02, automatiquement
il garantira aussi DF03,
sans qu'on lui impose explicitement le surcroît de travail qui résulterait
de notre ignorance de l'existence de I.
Le but de la manœuvre est donc de s'assurer que l'on demande au SGBD de veiller
au respect d'un ensemble irréductible de dépendances fonctionnelles, qu'on lui
soumet sous forme de contraintes. Comme on vient de le voir, il serait en effet dommage
de le surcharger inutilement à cause de
contraintes redondantes car pouvant être inférées.
3lignes.jpg) |
Maintenant, Jeff Ullman écrit :
« Étant donnés les ensembles de dépendances S et I,
ces ensembles sont équivalents si et seulement si chaque dépendance appartenant à S
appartient aussi à I+ et chaque dépendance appartenant à I appartient aussi
à S+ » ([Ullman 1982], « Covers of Sets of Dependencies »).
|
Concrètement, on doit donc chercher (s'il existe) le
plus petit sous-ensemble I de S
dont la fermeture I+ est égale à S+, pour ainsi se débarrasser de toutes
les DF inutiles en remplaçant S par I.
L'utilisation des seuls axiomes d'Armstrong et des règles qui en sont inférées
est évidemment possible pour résoudre
ce genre de problème, mais on perd le plus souvent beaucoup trop de temps, ne serait-ce
que pour traiter de
cas a priori réputés simples. Ainsi, après l'exemple que nous venons de voir,
considérons celui-ci :
Soit la relvar R {A,B,C,D} et l'ensemble S de DF
{{A,C,D} ➔ {B}, {C} ➔ {A}}.
La DF {A,C,D} ➔ {B} est réductible à {C,D} ➔ {B}, car par augmentation
{C} ➔ {A} engendre {C,D} ➔ {A,C,D}
et comme {A,C,D} ➔ {B}, par transitivité {C,D} ➔ {B}.
A moins de se sentir inspiré, on se munira d'un tube aspirine avant de se
lancer dans la résolution d'exercices un peu plus corsés. Mais heureusement,
on peut contourner les axiomes et règles
d'Armstrong. Il existe pour cela une alternative qui consiste à mettre
en oeuvre la méthode décrite
dans le paragraphe suivant (encore un genre de rouleau compresseur...)
N.B. Nous reprenons de Chris Date l'expression « ensemble irréductible »,
mais on trouve chez les auteurs des expressions équivalentes :
« couverture irréductible », « couverture minimale »,
« couverture irredondante », etc.)
E.6.2. Propriétés d'un ensemble irréductible de DF
Un ensemble I de dépendances fonctionnelles associé à une relvar R
est dit irréductible sous certaines conditions :
-
Le dépendant (partie droite) de chaque DF appartenant à I ne
doit contenir qu'un seul attribut.
-
Le déterminant D (partie gauche) de chaque DF doit être irréductible,
c'est-à-dire
qu'aucun attribut ne peut être éliminé de D
s'il en résulte une transformation de I en J telle que
J+ ≠ I+ par rapport à R.
Une telle DF est dite irréductible à gauche (left irreducible),
ou élémentaire ou totale.
(Se reporter aussi au paragraphe 3.2.2). Inversement,
si l'élimination d'un attribut
de D (ou plusieurs) donne lieu à une transformation de I en J telle que
J+ = I+, alors la DF est réductible.
-
Une DF ne peut être éliminée de I s'il en résulte une transformation de
I en J telle que J+ ≠ I+ par rapport à R.
3lignes.jpg) |
Le point 1 ne se justifie que pour faciliter la production de I. Une fois le travail terminé,
on pourra regrouper dans un même dépendant tous les dépendants singletons ayant même déterminant
(règle d'union).
Quand on traite du point 2, il se peut qu'on produise plus d'un ensemble irréductible
(ou candidat à l'irréductibilité).
Ainsi, étant donnée R {A,B,C} et l'ensemble de dépendances fonctionnelles
S = {{A,B} ➔ {C}, {A} ➔ {B}, {B} ➔ {A}},
on peut produire deux ensembles irréductibles :
I = {{A} ➔ {C}, {A} ➔ {B}, {B} ➔ {A}}
et J = {{B} ➔ {C}, {A} ➔ {B}, {B} ➔ {A}}.
Quand on traite du point 3, on peut là aussi produire plus d'un ensemble irréductible
(voir le paragraphe E.6.3, où l'on reprend l'exemple proposé par Ullman et dont on s'est déjà
servi au paragraphe E.5.1).
|
Illustration de la méthode
Pour bien comprendre la méthode utilisée en relation avec ces trois conditions
et aboutir à un résultat conforme,
servons-nous encore d'un exemple proposé par Chris Date.
Soit une relvar R {A,B,C,D} et S l'ensemble de DF
que l'on demande au système de garantir :
S = { {A} ➔ {B,C}
{B} ➔ {C}
{A} ➔ {B}
{A,B} ➔ {C}
{A,C} ➔ {D} }
|
Cherchons un ensemble irréductible I de DF.
Première étape
On transforme S, de telle sorte que le dépendant de chaque DF soit singleton
(application de la règle de décomposition) :
S = { DF01 : {A} ➔ {B}
DF02 : {A} ➔ {C}
DF03 : {B} ➔ {C}
DF04 : {A} ➔ {B}
DF05 : {A,B} ➔ {C}
DF06 : {A,C} ➔ {D} }
|
La DF {A} ➔ {B} étant présente deux fois,
on n'en conserve qu'une seule occurrence, disons DF01 :
S = { DF01 : {A} ➔ {B}
DF02 : {A} ➔ {C}
DF03 : {B} ➔ {C}
DF05 : {A,B} ➔ {C}
DF06 : {A,C} ➔ {D} }
|
Deuxième étape
On réduit le déterminant de chaque DF pour laquelle c'est possible :
|
|
Sont à considérer les DF dont le déterminant comporte plus d'un attribut,
à savoir DF05 et DF06.
a) Cas de DF05 :
{A,B} ➔ {C}.
|
|
|
DF05 est-elle réductible à {A} ➔ {C} ?
Considérons le sous-ensemble I de S, où l'on remplace DF05 par DF05a :
{A} ➔ {C}. S et I sont respectivement représentés par :
S = {
DF01 : {A} ➔ {B}
DF02 : {A} ➔ {C}
DF03 : {B} ➔ {C}
DF05 : {A,B} ➔ {C}
DF06 : {A,C} ➔ {D} }
I = {
DF01 : {A} ➔ {B}
DF02 : {A} ➔ {C}
DF03 : {B} ➔ {C}
DF05a : {A} ➔ {C}
DF06 : {A,C} ➔ {D} }
Par référence à Ullman (cf. paragraphe E.6.1) les ensembles S et I
sont équivalents si et seulement si chaque DF appartenant à S
appartient aussi à I+ et chaque DF appartenant à I appartient
aussi à S+.
Dans le cas de DF05 et DF05a, S et I sont donc équivalents
si et seulement si la fermeture
{A}+ de {A} par rapport à S est égale à la fermeture
{A}+ de {A} par rapport à I.
S'il y a inégalité, cela est dû à la composition différente des
déterminants de DF05 et DF05a (seules DF à présenter une différence).
De fait,
contrairement au déterminant {A} de DF05a, la partie {A}
du déterminant {A,B} de DF05 ne permet pas à elle seule de
capturer l'attribut C : si possible, une autre DF devra
compenser pour rattraper le coup.
Qu'en est-il ? Au moyen de l'algorithme du seau,
calculons {A}+ par rapport à S :
{A}+ = {A}, puis {A,B} du fait de DF01, puis {A,B,C} du fait de DF02,
puis {A,B,C,D} du fait de DF06.
De même, calculons {A}+ par rapport à I :
{A}+ = {A}, puis {A,B} du fait de DF01, puis {A,B,C} du fait de DF02,
puis {A,B,C,D} du fait de DF06.
On constate ainsi que {A}+ par rapport à S égale {A}+ par rapport à I :
Les deux ensembles S et I sont équivalents par rapport
à leurs fermetures et I peut donc remplacer S.
Comme par ailleurs DF05a existe déjà en tant que DF02
(ce qui fait qu'on aurait pu se dispenser de calculer, mais il faut bien illustrer la méthode),
l'ensemble S se réduit à :
S = { DF01 : {A} ➔ {B}
DF02 : {A} ➔ {C}
DF03 : {B} ➔ {C}
DF06 : {A,C} ➔ {D} }
A noter que, grâce à DF03, DF05 était aussi réductible à
{B} ➔ {C}. En effet, partant de DF03, par augmentation on produit
{A,B} ➔ {A,C}, puis par décomposition on produit
{A,B} ➔ {C}, c'est-à-dire DF05.
|
|
|
b) Cas de DF06 :
{A,C} ➔ {D}.
|
|
|
DF06 est-elle réductible à {A} ➔ {D} ?
Considérons le sous-ensemble I de S, dans lequel on remplace
DF06 par DF06a : {A} ➔ {D}.
Les deux ensembles S et I sont équivalents si et
seulement si
la fermeture {A}+ de {A} par rapport à S est égale à la
fermeture {A}+ de {A} par rapport à I.
S et I sont respectivement représentés par :
S = {
DF01 : {A} ➔ {B}
DF02 : {A} ➔ {C}
DF03 : {B} ➔ {C}
DF06 : {A,C} ➔ {D} }
I = {
DF01 : {A} ➔ {B}
DF02 : {A} ➔ {C}
DF03 : {B} ➔ {C}
DF06a : {A} ➔ {D} }
DF06a ayant pour déterminant {A}, les deux ensembles S et I sont
équivalents si et seulement si la fermeture {A}+ de {A} par
rapport à S est égale à la fermeture {A}+ de {A}
par rapport à I.
Au moyen de l'algorithme du seau, calculons {A}+ par rapport à S :
{A}+ = {A}, puis {A,B} du fait de DF01, puis {A,B,C} du fait de
DF02, puis {A,B,C,D} du fait de DF06.
De même, calculons {A}+ par rapport à I :
{A}+ = {A}, puis {A,B} du fait de DF01, puis {A,B,C} du fait de
DF02, puis {A,B,C,D} du fait de DF06a.
{A}+ par rapport à S est égal à {A}+ par rapport à I :
Les deux ensembles S et I sont équivalents par rapport à
leurs fermetures et I peut donc remplacer S qui devient :
S = { DF01 : {A} ➔ {B}
DF02 : {A} ➔ {C}
DF03 : {B} ➔ {C}
DF06a : {A} ➔ {D} }
Pour sa part, DF06 n'est pas réductible à {C} ➔ {D},
car les fermetures
{C}+ par rapport à I : {C,D} et {C}+ par rapport à
S : {C} ne sont pas égales.
|
Troisième étape
On cherche quelles DF peuvent disparaître, sans conséquence sur S.
|
|
a) Commençons par tenter de supprimer la 1re DF qui se présente,
à savoir DF01 pour réduire S à I = S — {DF01}.
Concernant S, DF01 a pour déterminant {A}. En utilisant l'algorithme du
seau, calculons la fermeture {A}+ par rapport à S.
Au départ, {A}+ = {A}.
Ensuite, {A}+ = {A,B}
du fait de DF01 (présente dans S), puis {A,B,C} du fait de DF02,
puis {A,B,C,D} du fait de DF06a.
Calculons la fermeture {A}+ par rapport à I.
Au départ, {A}+ = {A}.
Ensuite, {A}+ = {A,C} du fait de DF02,
puis {A,C,D} du fait de DF06a, puis plus rien ne se passe
puisque DF01 est absente de I.
{A}+ par rapport à S diffère de {A}+ par rapport à I,
donc DF01 ne peut pas être éliminée de S.
b) Tentons de supprimer la DF suivante, DF02 pour réduire S à
I = S — {DF02}.
Concernant S, DF02 a pour déterminant {A}.
En utilisant l'algorithme du
seau, calculons la fermeture {A}+ par rapport à S.
Au départ, {A}+ = {A}.
Ensuite, {A}+ = {A,B} du fait de DF01,
puis {A,B,C} du fait de DF02 (présente dans S),
puis {A,B,C,D} du fait de DF06a.
Calculons la fermeture {A}+ par rapport à I.
Au départ, {A}+ = {A}.
Ensuite, {A}+ = {A,B} du fait de
DF01, puis {A,B,C} du fait de DF03,
puis {A,B,C,D} du fait de DF06a.
{A}+ par rapport à S égale {A}+ par rapport à I,
donc DF02 peut être éliminée de S qui devient :
S = { DF01 : {A} ➔ {B}
DF03 : {B} ➔ {C}
DF06a : {A} ➔ {D} }
L'ensemble de DF est maintenant irréductible.
En effet, on a déjà montré que
DF01 ne pouvait pas être supprimée.
Sans même calculer, on sait que
DF03 ne peut pas l'être non plus, car
l'attribut C fait partie de sa fermeture {B}+ mais est
absent de DF01 et de DF06a. A son tour DF06a ne peut
pas non plus être supprimée,
car l'attribut D fait partie de sa fermeture {A}+
mais est absent de DF01 et de DF03.
|
Le travail est terminé et, de façon mécanique, on a réduit l'ensemble
S de DF de la relvar R de façon conséquente.
 |
Plutôt qu'utiliser l'algorithme du seau on aurait pu en passer par
les axiomes d'Armstrong et les règles qui en sont inférées,
mais on conviendra que la tâche devient d'autant plus ardue que l'on manque d'entraînement.
|
Ainsi, revenons-en à l'ensemble des DF obtenu après la première étape :
DF01 : {A} ➔ {B}
DF02 : {A} ➔ {C}
DF03 : {B} ➔ {C}
DF05 : {A,B} ➔ {C}
DF06 : {A,C} ➔ {D}
|
Concernant la 2e étape :
a) Montrer que la DF {A,B} ➔ {C} peut être inférée
1 {A} ➔ {C}
(donné)
2 {A,B} ➔ {B,C}
(1, augmentation)
3 {A,B} ➔ {C}
(2, décomposition)
|
b) Montrer que la DF {A} ➔ {D} peut être inférée
1 {A} ➔ {C}
(donné)
2 {A} ➔ {A,C}
(1, augmentation)
3 {A,C} ➔ {D}
(donné)
4 {A} ➔ {D}
(2, 3, transitivité)
|
Concernant la 3e étape :
Montrer que la DF {A} ➔ {C} peut être inférée
1 {A} ➔ {B}
(donné)
2 {B} ➔ {C}
(donné)
3 {A} ➔ {C}
(1, 2, transitivité)
|
A chacun sa stratégie : se passer d'un rouleau compresseur rustique et d'un seau à dépendants,
préférer mettre en œuvre les axiomes d'Armstrong est certes plus élégant.
En tout cas, l'essentiel est que le travail soit mené à bien.
E.6.3. Pluralité des ensembles irréductibles pour une relvar
Pour une relvar et un ensemble donné de DF, on peut avoir plus d'un ensemble irréductible.
Reprenons l'exemple proposé par Ullman (cf. annexe E.5.1).
L'ensemble S des DF pour la relvar R {A,B,C,D,E,G} est le suivant :
|
|
S = { DF01 : {A,B} ➔ {C}
DF05 : {D} ➔ {E,G}
DF02 : {C} ➔ {A}
DF06 : {B,E} ➔ {C}
DF03 : {B,C} ➔ {D}
DF07 : {C,G} ➔ {B,D}
DF04 :
{A,C,D} ➔ {B}
DF08 : {C,E} ➔ {A,G} }
|
Cherchons à réduire S.
Première étape
On transforme S, de telle sorte que le dépendant de chaque DF soit singleton
(application de la règle de décomposition) :
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 : {A,C,D} ➔ {B}
DF05 : {D} ➔ {E}
DF06 : {D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
Deuxième étape
Quand c'est possible, on réduit le déterminant de chaque DF :
|
|
Sont à considérer les DF dont le déterminant comporte plus d'un attribut,
à savoir DF01, DF03, DF04, DF07, DF08, DF09, DF10, DF11.
a) Cas de DF01 : {A,B} ➔ {C}.
|
|
|
DF01 est-elle réductible à {A} ➔ {C} ?
Considérons le sous-ensemble I de S, où l'on remplace
DF01 par DF01a , {A} ➔ {C} :
|
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 :
{A,C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
I = { DF01a : {A} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 :
{A,C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
DF01a a pour déterminant {A}.
Les deux ensembles S et I sont équivalents si et
seulement si la fermeture {A}+ de {A} par rapport à S
est égale à la
fermeture {A}+ de {A} par rapport à I.
Au moyen de l'algorithme du seau, calculons {A}+ par
rapport à S :
{A}+ = {A}, puis on en reste là.
Calculons {A}+ par rapport à I : {A}+ = {A,C} du fait de DF01a.
{A}+ par rapport à S n'est pas égal à {A}+ par rapport à I :
S ne peut pas être remplacé par I.
DF01 est-elle réductible à {B} ➔ {C} ?
Considérons le sous-ensemble I de S, où l'on remplace
DF01 par DF01b , {B} ➔ {C} :
|
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 :
{A,C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
I = { DF01b : {B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 :
{A,C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
DF01b a pour déterminant {B}. Les deux ensembles S et I
sont équivalents si et
seulement si la fermeture {B}+ de {B} par rapport à S est égale à la
fermeture {B}+ de {B} par rapport à I.
Au moyen de l'algorithme du seau, calculons {B}+
par rapport à S :
{B}+ = {B}, puis on en reste là.
Calculons {B}+ par rapport à I :
{B}+ = {B,C} du fait de DF01a, puis {B,C,D} du fait de DF03, etc.
{B}+ par rapport à S n'est pas égal à {B}+
par rapport à I :
S ne peut pas être remplacé par I.
|
b) Cas de DF03 : {B,C} ➔ {D}.
|
|
DF03 est-elle réductible à {B} ➔ {D} ?
Considérons le sous-ensemble I de S, où l'on remplace
DF03 par DF03a, {B} ➔ {D} :
|
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 :
{A,C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
I = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03a : {B} ➔ {D}
DF04 :
{A,C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
DF03a a pour déterminant {B}.
Les deux ensembles S et I sont équivalents si et
seulement si la fermeture {B}+ de {B} par rapport à S
est égale à la
fermeture {B}+ de {B} par rapport à I.
Au moyen de l'algorithme du seau, calculons {B}+ par
rapport à S :
{B}+ = {B}, puis on en reste là.
Calculons {B}+ par rapport à I : {B}+ = {B,D} du fait de DF03a,
puis {B,D,E} du fait de DF05, etc.
{B}+ par rapport à S n'est pas égal à {B}+ par rapport à I :
S ne peut pas être remplacé par I.
DF03 est-elle réductible à {C} ➔ {D} ?
Considérons le sous-ensemble I de S, où l'on remplace
DF03 par DF03b, {C} ➔ {D} :
|
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 :
{A,C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
I = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03b : {C} ➔ {D}
DF04 :
{A,C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
DF03b a pour déterminant {C}. Les deux ensembles S et I
sont équivalents si et
seulement si la fermeture {C}+ de {C} par rapport à S est égale à la
fermeture {C}+ de {C} par rapport à I.
Calculons {C}+
par rapport à S :
{C}+ = {A,C} du fait de DF02, puis on en reste là.
Calculons {C}+ par rapport à I :
{C}+ = {C,D} du fait de DF03b, puis {A,C,D} du fait de DF02, etc.
{B}+ par rapport à S n'est pas égal à {B}+
par rapport à I qui ne peut donc pas remplacer S.
|
c) Cas de DF04 : {A,C,D} ➔ {B}.
|
|
DF04 est-elle réductible à {A,C} ➔ {B} ?
Considérons le sous-ensemble I de S, où l'on remplace
DF04 par DF04a, {A,C} ➔ {B} :
|
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 :
{A,C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
I = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04a :
{A,C} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
DF04a a pour déterminant {A,C}.
Les deux ensembles S et I sont équivalents si et
seulement si la fermeture {A,C}+ de {A,C} par rapport à S
est égale à la
fermeture {A,C}+ de {A,C} par rapport à I.
Calculons {A,C}+ par
rapport à S :
{A,C}+ = {A,C}, puis on en reste là.
Calculons {A,C}+ par rapport à I : {A,C}+ = {A,B,C}
du fait de DF04a,
puis {A,B,C,D} du fait de DF03, etc.
{A,C}+ par rapport à S n'est pas égal à {A,C}+ par rapport à I
qui ne peut donc pas remplacer S.
DF04 est-elle réductible à {A,D} ➔ {B} ?
Considérons le sous-ensemble I de S, où l'on remplace
DF04 par DF04b, {A,D} ➔ {B} :
|
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 :
{A,C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
I = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04b :
{A,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
DF04b a pour déterminant {A,D}. Les deux ensembles S et I
sont équivalents si et
seulement si la fermeture {A,D}+ de {A,D} par rapport à S est égale à la
fermeture {A,D}+ de {A,D} par rapport à I.
Calculons {A,D}+
par rapport à S :
{A,D}+ = {A,D}, puis {A,D,E,G} du fait de DF05 et DF06.
Calculons {A,D}+ par rapport à I :
{A,D}+ = {A,B,D} du fait de DF04b, puis {A,B,C,D} du fait de DF01, etc.
{A,D}+ par rapport à S n'est pas égal à {A,D}+
par rapport à I qui ne peut donc pas remplacer S.
DF04 est-elle réductible à {C,D} ➔ {B} ?
Considérons le sous-ensemble I de S, où l'on remplace
DF04 par DF04c, {C,D} ➔ {B} :
|
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 :
{A,C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
I = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04c :
{C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF10 : {C,E} ➔ {A}
DF11 : {C,E} ➔ {G} }
|
|
|
DF04c a pour déterminant {C,D}. Les deux ensembles S et I
sont équivalents si et
seulement si la fermeture {C,D}+ de {C,D} par rapport à S est égale à la
fermeture {C,D}+ de {C,D} par rapport à I.
Calculons {C,D}+
par rapport à S :
{C,D}+ = {C,D}, puis {A,C,D} du fait de DF02,
puis {A,C,D,E,G} du fait de DF05 et DF06,
puis {A,B,C,D,E,G} du fait de DF08 (on notera que {C,D}
représente une clé candidate pour R).
Calculons {C,D}+ par rapport à I :
{C,D}+ = {B,C,D} du fait de DF04c,
puis {A,B,C,D} du fait de DF01, puis {A,B,C,D,E,G}
du fait de DF05 et DF06.
|
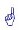 |
{C,D}+ par rapport à S est égal à {C,D}+ par rapport à I :
S peut être remplacé par I et la dépendance fonctionnelle DF04 par D04c
= {C,D} ➔ {B}.
Mais le déterminant de DF04c
comporte deux attributs et il faut donc vérifier si, à son tour,
cette DF peut se
simplifier en {C} ➔ {B} ou {D} ➔ {B}.
|
|
|
Concernant {C} ➔ {B}, la fermeture {C}+ par
rapport à S est égale à {A,C} et la fermeture {C}+ par
rapport à I est égale à {A,B,C,D,E,G}. Ces fermetures ne sont pas égales,
donc la simplification n'est pas possible.
Concernant {D} ➔ {B}, la fermeture {D}+ par
rapport à S est égale à {D,E,G} et la fermeture {C}+ par rapport
à I est égale à {A,B,C,D,E,G} : Ces fermetures n'étant pas égales,
la simplification n'est pas possible.
|
d)
Cas de DF07 à DF11 :
|
|
Toujours avec la même méthode, on montre ensuite que ces dépendances fonctionnelles sont
irréductibles, à l'exception de DF10 pour laquelle {C}+ par rapport à S est égale à {C}+
par rapport à I. DF10 est réductible à {C} ➔ {A} c'est-à-dire à
DF02 : DF10 disparaît.
|
En fin d'étape 2, l'ensemble S à été réduit à :
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 : {C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF11 : {C,E} ➔ {G} }
|
Troisième étape
On cherche quelles DF peuvent disparaître, sans conséquence pour S.
Commençons par tenter de supprimer la 1re DF qui se présente,
à savoir DF01 pour réduire S à I = S — {DF01}.
|
|
Concernant S, le déterminant {A,B} de DF01 a
d'abord pour fermeture {A,B}+ = {A,B,C} — du fait de DF01 elle-même —,
puis {A,B,C,D} du fait de DF03, puis {A,B,C,D,E,G} du
fait de DF05 et DF06.
Concernant I, on cherche donc à retrouver
{A,B}+ = {A,B,C,D,E,G}
sans utiliser DF01. Au départ, {A,B}+ = {A,B}, mais rien
d'autre ne
peut tomber dans le seau :
{A,B}+ par rapport à S n'est pas égal à {A,B}+ par rapport à I,
donc DF01 doit continuer à faire partie de S.
|
Tentons de supprimer la DF suivante, à savoir DF02 pour réduire S
à I = S — {DF02}.
|
|
Concernant S, le déterminant {C} de DF02 a
d'abord pour fermeture {C}+ = {A,C} — du fait de DF02 elle-même —,
mais rien d'autre ne
peut tomber dans le seau.
Concernant I, on cherche à retrouver
{C}+ = {A,C}
sans utiliser DF02. Au départ, {C}+ = {C}, mais rien
d'autre ne peut tomber dans le seau :
{C}+ par rapport à S n'est pas égal à {C}+ par rapport à I,
donc DF02 doit continuer à faire partie de S.
|
Tentons de supprimer la DF suivante, à savoir DF03 pour réduire S
à I = S — {DF03}.
|
|
Concernant S, le déterminant {B,C} de DF03 a
d'abord pour fermeture {B,C}+ = {B,C,D} — du fait de DF03 elle-même —,
puis {A,B,C,D} du fait de DF02, puis {A,B,C,D,E,G} du
fait de DF05 et DF06.
Concernant I, on cherche à retrouver
{B,C}+ = {A,B,C,D,E,G}
sans utiliser DF03. Au départ, {B,C}+ = {B,C},
puis {A,B,C} du fait de DF02, mais sans DF03
rien d'autre ne peut tomber dans le seau :
{B,C}+ par rapport à S n'est pas égal à {B,C}+ par rapport à I,
donc DF03 doit continuer à faire partie de S.
|
Tentons de supprimer la DF suivante, à savoir DF04 pour réduire S
à I = S — {DF04}.
|
|
Concernant S, le déterminant {C,D} de DF04 a
d'abord pour fermeture {C,D}+ = {B,C,D} — du fait de DF04 elle-même —,
puis {A,B,C,D} du fait de DF02, puis {A,B,C,D,E,G} du
fait de DF05 et DF06.
Concernant I, on cherche à retrouver
{C,D}+ = {A,B,C,D,E,G}
sans utiliser DF04. Au départ, {C,D}+ = {C,D},
puis {A,C,D} du fait de DF02, puis {A,C,D,E,G} du fait de DF05 et DF06,
puis {A,B,C,D,E,G} du fait de DF08 :
{C,D}+ par rapport à S est égal à {C,D}+ par rapport à I,
donc DF04 peut disparaître
(puisque I comporte la
DF {C,D} ➔ {A,B,C,D,E,G}, en
vertu de la règle de décomposition on infère la
DF {C,D} ➔ {B}).
Dans ces conditions, S devient :
|
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF11 : {C,E} ➔ {G} }
|
Tentons de supprimer la DF suivante, à savoir DF05 pour réduire S
à I = S — {DF05}.
|
|
Concernant S, le déterminant {D} de DF05 a
d'abord pour fermeture {D}+ = {D,E} — du fait de DF05 elle-même —,
puis {D,E,G} du fait de DF06,
mais rien d'autre ne
peut tomber dans le seau.
Concernant I, on cherche à retrouver
{D}+ = {D,E,G}
sans utiliser DF05. Au départ, {D}+ = {D},
puis {D,G} du fait de DF06,
mais rien
d'autre ne peut tomber dans le seau :
{D}+ par rapport à S n'est pas égal à {D}+ par rapport à I,
donc DF05 doit continuer à faire partie de S.
|
Tentons de supprimer la DF suivante, à savoir DF06 pour réduire S
à I = S — {DF06}.
|
|
Concernant S, le déterminant {D} de DF06 a
d'abord pour fermeture {D}+ = {D,G} — du fait de DF06 elle-même —,
puis {D,E,G} du fait de DF05,
mais rien d'autre ne
peut tomber dans le seau.
Concernant I, on cherche à retrouver
{D}+ = {D,E,G}
sans utiliser DF06. Au départ, {D}+ = {D},
puis {D,E} du fait de DF05,
mais rien
d'autre ne peut tomber dans le seau :
{D}+ par rapport à S n'est pas égal à {D}+ par rapport à I,
donc DF06 doit continuer à faire partie de S.
|
Tentons de supprimer la DF suivante, à savoir DF07 pour réduire S
à I = S — {DF07}.
|
|
Concernant S, le déterminant {B,E} de DF07 a
d'abord pour fermeture {B,E}+ = {B,C,E} — du fait de DF07 elle-même —,
puis {A,B,C,E} du fait de DF02,
puis {A,B,C,D,E} du fait de DF03,
puis {A,B,C,D,E,G} du fait de DF06.
Concernant I, on cherche à retrouver
{B,E}+ = {A,B,C,D,E,G}
sans utiliser DF07. Au départ, {B,E}+ = {B,E},
mais rien
d'autre ne peut tomber dans le seau :
{B,E}+ par rapport à S n'est pas égal à {B,E}+ par rapport à I,
donc DF07 doit continuer à faire partie de S.
|
Tentons de supprimer la DF suivante, à savoir DF08 pour réduire S
à I = S — {DF08}.
|
|
Concernant S, le déterminant {C,G} de DF08 a
d'abord pour fermeture {C,G}+ = {B,C,G} — du fait de DF08 elle-même —,
puis {A,B,C,G} du fait de DF02,
puis {A,B,C,D,G} du fait de DF03,
puis {A,B,C,D,E,G} du fait de DF05.
Concernant I, on cherche à retrouver
{C,G}+ = {A,B,C,D,E,G}
sans utiliser DF08. Au départ, {C,G}+ = {C,G},
puis {A,C,G} du fait de DF02,
puis {A,C,D,G} du fait de DF09,
puis {A,C,D,E,G} du fait de DF05,
mais rien
d'autre ne peut tomber dans le seau :
{C,G}+ par rapport à S n'est pas égal à {C,G}+ par rapport à I,
donc DF08 doit continuer à faire partie de S.
|
Tentons de supprimer la DF suivante, à savoir DF09 pour réduire S
à I = S — {DF09}.
|
|
Concernant S, le déterminant {C,G} de DF09 a
d'abord pour fermeture {C,G}+ = {C,D,G} — du fait de DF09 elle-même —,
puis {A,C,D,G} du fait de DF02,
puis {A,C,D,E,G} du fait de DF05,
puis {A,B,C,D,E,G} du fait de DF08.
Concernant I, on cherche à retrouver
{C,G}+ = {A,B,C,D,E,G}
sans utiliser DF09. Au départ, {C,G}+ = {C,G},
puis {A,C,G} du fait de DF02, puis {A,B,C,G} du fait de DF08,
puis {A,B,C,D,G} du fait de DF03,
puis {A,B,C,D,E,G} du fait de DF05 :
{C,G}+ par rapport à S est égal à {C,G}+ par rapport à I,
donc DF09 peut disparaître
(puisque I comporte la
DF {C,G} ➔ {A,B,C,D,E,G}, en
vertu de la règle de décomposition on infère la
DF {C,G} ➔ {D}).
Dans ces conditions, S devient :
|
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF11 : {C,E} ➔ {G} }
|
Tentons de supprimer la DF suivante, à savoir DF11 pour réduire S
à I = S — {DF11}.
|
|
Concernant S, le déterminant {C,E} de DF11 a
d'abord pour fermeture {C,E}+ = {C,E,G} — du fait de DF11 elle-même —,
puis {A,C,E,G} du fait de DF02,
puis {A,B,C,E,G} du fait de DF08,
puis {A,B,C,D,E,G} du fait de DF03.
Concernant I, on cherche à retrouver
{C,E}+ = {A,B,C,D,E,G}
sans utiliser DF11. Au départ, {C,E}+ = {C,E},
puis {A,C,E} du fait de DF02,
mais rien
d'autre ne peut tomber dans le seau :
{C,E}+ par rapport à S n'est pas égal à {C,E}+ par rapport à I,
donc DF11 doit continuer à faire partie de S.
|
C'est fini
Il n'y a plus d'autre DF à chercher à éliminer :
l'ensemble S proposé pour la 3e étape était réductible
du fait de la présence de DF redondantes :
DF04 = {A,C,D} ➔ {B}
(réduite d'abord à {C,D} ➔ {B} ce qui du reste n'était pas indispensable)
et DF09 = {C,G} ➔ {D}.
S est maintenant irréductible.
1er ensemble irréductible :
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF11 : {C,E} ➔ {G} }
|
3lignes.jpg) |
Rappelons en passant que {A,B}, {B,C}, {B,D}, {B,E}, {C,D}, {C,E}, {C,G} sont les clés
candidates de la relvar R (Cf. paragraphe E.5.2).
Par ailleurs, les dépendants singletons ayant même
déterminant peuvent maintenant être regroupés : {D} ➔ {E,G}.
|
Recherche d'un autre ensemble irréductible
Un ensemble irréductible n'est pas nécessairement unique et, dans cet exemple,
tout peut dépendre de l'ordre dans lequel on élimine les redondances.
Reprenons la 3e étape à son début :
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 : {C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF08 : {C,G} ➔ {B}
DF09 : {C,G} ➔ {D}
DF11 : {C,E} ➔ {G} }
|
Et commençons par chercher à éliminer DF08 : {C,G} ➔ {B}
pour réduire S à I = S — {DF08}.
|
|
Concernant S, le déterminant {C,G} de DF08 a
d'abord pour fermeture {C,G}+ = {B,C,G} — du fait de DF08 elle-même —,
puis {A,B,C,G} du fait de DF02,
puis {A,B,C,D,G} du fait de DF03,
puis {A,B,C,D,E,G} du fait de DF05.
Concernant I, on cherche à retrouver
{C,G}+ = {A,B,C,D,E,G}
sans utiliser DF08. Au départ, {C,G}+ = {C,G},
puis {A,C,G} du fait de DF02,
puis {A,C,D,G} du fait de DF09,
puis {A,B,C,D,G} du fait de DF04
(ce qui n'avait pas été possible lors du tour précédent,
DF04 ayant d'abord été éliminée de S),
puis {A,B,C,D,E,G} du fait de DF05 :
{C,G}+ par rapport à S est égal à {C,G}+ par rapport à I,
donc DF08 peut disparaître
(puisque I comporte la
DF {C,G} ➔ {A,B,C,D,E,G}, en
vertu de la règle de décomposition on infère la
DF {C,G} ➔ {B}).
Dans ces conditions, S devient :
|
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 : {C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF09 : {C,G} ➔ {D}
DF11 : {C,E} ➔ {G} }
|
|
|
On sait désormais que le nouvel ensemble est nécessairement différent
du 1er ensemble irréductible, puisque que l'on vient d'éliminer DF08 qui fait partie du 1er.
On repart pour un tour complet,
et l'on montre à nouveau que DF01, DF02, DF03, DF05, DF06, DF07 et DF11
ne sont pas redondantes et ne peuvent pas être éliminées. Mais on montre
aussi que DF04 et DF09, qui ne font pas partie du 1er ensemble irréductible,
ne pourront pas cette fois-ci être éliminées.
Cas de DF04 :
|
|
|
Concernant S, le déterminant {C,D} de DF04 a
d'abord pour fermeture {C,D}+ = {B,C,D} — du fait de DF04 elle-même —,
puis {A,B,C,D} du fait de DF02,
puis {A,B,C,D,E,G} du fait de DF05 et DF06.
Concernant I, on cherche à retrouver
{C,D}+ = {A,B,C,D,E,G}
sans utiliser DF04. Au départ, {C,D}+ = {C,D},
puis {A,C,D} du fait de DF02,
puis {A,C,D,E,G} du fait de DF05 et DF06,
mais rien
d'autre ne peut tomber dans le seau
(outre la tentative d'élimination de DF04, comme on vient
de procéder à celle de DF08, l'attribut B ne peut plus être capturé)
:
{C,D}+ par rapport à S n'est pas égal à {C,D}+ par rapport à I,
donc DF04 doit continuer à faire partie de S.
|
Cas de DF09 :
|
|
Concernant S, le déterminant {C,G} de DF09 a
d'abord pour fermeture {C,G}+ = {C,D,G} — du fait de DF09 elle-même —,
puis {A,C,D,G} du fait de DF02,
puis {A,B,C,D,G} du fait de DF04,
puis {A,B,C,D,E,G} du fait de DF05.
Concernant I, on cherche à retrouver
{C,G}+ = {A,B,C,D,E,G}
sans utiliser DF09. Au départ, {C,G}+ = {C,G},
puis {A,C,G} du fait de DF02,
mais rien
d'autre ne peut tomber dans le seau
(outre la tentative d'élimination de DF09, comme on vient
de procéder à celle de DF08, l'attribut B ne peut plus être capturé)
:
{C,G}+ par rapport à S n'est pas égal à {C,G}+ par rapport à I,
donc DF09 doit continuer à faire partie de S.
|
Ainsi, on dispose d'un deuxième ensemble irréductible :
Deuxième ensemble irréductible :
|
|
S = { DF01 : {A,B} ➔ {C}
DF02 : {C} ➔ {A}
DF03 : {B,C} ➔ {D}
DF04 : {C,D} ➔ {B}
DF05 :
{D} ➔ {E}
DF06 :
{D} ➔ {G}
DF07 : {B,E} ➔ {C}
DF09 : {C,G} ➔ {D}
DF11 : {C,E} ➔ {G} }
|
On a détaillé le plus possible une technique de recherche des ensembles irréductibles.
On laissera aux plus astucieux ou courageux le soin de vérifier
s'il existe d'autres ensembles irréductibles.
On peut aussi, à l'aide de son langage préféré, développer un programme idoine
pour traiter ensuite le problème en un clic de souris. Quoi qu'il en soit, le but
de la manœuvre est bien de chercher à réduire S, afin d'éliminer les DF redondantes
et réduire ainsi la charge de travail du SGBD quant aux contrôles qu'on lui demandera d'assumer.
E.7. Décompositions sans perte
E.7.1. Préservation du contenu de la base de données
La stricte application du théorème de Heath permet de préserver le contenu de la base
de données quand on décompose une relvar. Voici une extension de ce théorème
(cf. [Ullman 1982], « Theorem 7.5 ») :
|
|
Si ρ = (R1, R2) est une décomposition de R, et S est un ensemble de
dépendances fonctionnelles, alors ρ préserve le contenu de la base de données
par rapport à S si et seulement si on vérifie les dépendances fonctionnelles :
(R1  R2) ➔ (R1 — R2)
ou
(R1 R2) ➔ (R1 — R2)
ou
(R1  R2) ➔ (R2 — R1). R2) ➔ (R2 — R1).
Ces dépendances n'appartiennent pas nécessairement à S, il suffit qu'elles appartiennent à S+.
|
Considérons par exemple la relvar suivante : R {A,B,C} et l'ensemble de DF associé :
S = {{A} ➔ {B}}.
Si on décompose R en R1 {A,B} et R2 {A,C}, le contenu de la base de données est préservé,
car d'une part
{A,B}

{A,C} = {A}
et d'autre part
{A,B} — {A,C} = {B}, donc on vérifie bien {A} ➔ {B}.
En revanche, si l'on décompose R en R1 {A,B} et R2 {B,C}, alors
{A,B}

{B,C} = {B},
{A,B} — {B,C} = {A} et {B,C} — {A,B} = {C} :
(R1

R2) ne détermine fonctionnellement
ni (R1 — R2) ni (R2 — R1), le contenu de la base de données n'est
donc pas préservé. On peut du reste le vérifier à l'aide d'un exemple :
|
|
Soit r = {{a1,b1,c1}, {a2,b1,c2}} une valeur prise par R. Les projections
R1 = 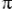 AB(r) et
R2 = AB(r) et
R2 = 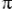 BC(r)
sont respectivement égales à {{a1,b1}, {a2,b1}} et {{b1,c1}, {b1,c2}}
tandis que leur jointure naturelle est égale à
{{a1,b1,c1}, {a1,b1,c2}, {a2,b1,c1}, {a2,b1,c2}}, laquelle n'est pas égale à r. BC(r)
sont respectivement égales à {{a1,b1}, {a2,b1}} et {{b1,c1}, {b1,c2}}
tandis que leur jointure naturelle est égale à
{{a1,b1,c1}, {a1,b1,c2}, {a2,b1,c1}, {a2,b1,c2}}, laquelle n'est pas égale à r.
|
Maintenant, peut-on produire des décompositions préservant le contenu de la base de données
sans appliquer le théorème de Heath ? Pour répondre à cette question, intéressons-nous à
un exemple proposé par Jeff Ullman (cf. [Ullman 1982], « Algorithm 7.2,
Testing Lossless Joins ») :
Soit la relvar R {A,B,C,D,E}. L'ensemble S de DF associé est le suivant :
S = {{A} ➔ {C}, {B} ➔ {C},
{C} ➔ {D}, {D,E} ➔ {C}, {C,E} ➔ {A}}
Et la décomposition proposée est la suivante :
ρ = ({A,D}, {A,B}, {C,D,E}, {A,E}, {B,E})
La méthode proposée de vérification de la préservation est la suivante :
on met en oeuvre un tableau dans lequel chaque colonne correspond à un attribut de R et
chaque ligne correspond à un élément de
ρ.
Soit A
j le nom de l'attribut figurant dans la colonne
j
et R
i le nom de l'élément figurant dans la ligne
i.
Si A
j appartient à R
i alors à l'intersection de la
ligne
i et de la colonne
j on fait figurer le symbole
aj.
Si A
j n'appartient pas à R
i alors à cette intersection
on fait figurer le symbole
bij :
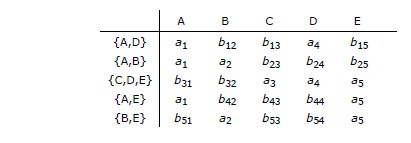
A partir de là, on applique un algorithme permettant de faire évoluer le contenu du tableau
en fonction des DF figurant dans S, le but étant d'arriver à mettre en évidence une ligne
qui ne contienne que des symboles
aj auquel cas
— et seulement dans ce cas — on pourra affirmer que
la décomposition préserve le contenu de la base de données (démonstration : voir le
théorème 7.4 figurant dans [Ullman 1982]).
Utilisons la 1re DF appartenant à S, {A} ➔ {C}. Dans le tableau ci-dessus, l'attribut A
(1re colonne) appartient au déterminant de la DF et comporte le même symbole
a1 aux lignes
1, 2 et 4. Selon l'algorithme, parce que l'attribut C (3e colonne du tableau) appartient
au dépendant de la DF, pour ces trois lignes on peut se limiter à un seul et même symbole,
qui peut être arbitrairement
b13,
b23 ou
b43.
Retenons
b13 auquel cas le tableau devient :

On utilise la même technique avec la DF suivante, {B} ➔ {C}. Du fait que
l'attribut B comporte deux fois le symbole
a2 (lignes 2 et 5),
le symbole
b13 (ligne 2) peut remplacer le symbole
b53
(ligne 5) :
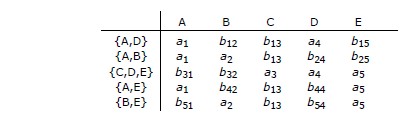
Même chose avec la DF suivante, {C} ➔ {D}. Du fait que l'attribut C comporte
quatre fois le symbole
b13 (lignes 1, 2, 4 et 5), le symbole
a4
(ligne 1) peut remplacer les symboles
b24 (ligne 2),
b44
(ligne 4) et
b54 (ligne 5) :
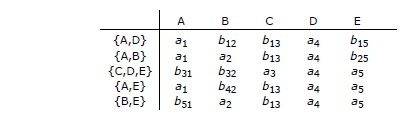
Avec la DF suivante, {D,E} ➔ {C}, on a trois fois la paire de
symboles <
a4,
a5>
(lignes 3, 4, 5) pour la paire de colonnes {D,E}. Le symbole a
3 (ligne 3) peut
remplacer le symbole
b13 (lignes 4 et 5) :

Avec la DF {C,E} ➔ {A}, on a trois fois la paire de symboles
<
a3,
a5>
(lignes 3, 4, 5) pour la paire de colonnes {C,E}. Le symbole
a1 (ligne 4)
peut remplacer les symboles
b31 (ligne 3) et
b51 (ligne 5) :

La dernière ligne du tableau ne comporte que des symboles
ai :
la décomposition préserve le contenu de la base de données, mais attention, il est possible qu'elle
ne préserve pas les dépendances fonctionnelles (cf. paragraphe suivant),
donc certaines règles de gestion des données que ces dépendances représentent...
E.7.2. Préservation des dépendances fonctionnelles
Reprenons la règle de pseudo-transitivité présentée au paragraphe E.2
et qui nous a servi pour présenter la réduction des ensembles de DF :
Si {A} ➔ {B} et {B,C} ➔ {D}, alors {A,C} ➔ {D}
A partir de là, définissons une relvar R{A,B,C,D} à laquelle est associé
le même ensemble S de DF :
S = {{A} ➔ {B}, {B,C} ➔ {D}, {A,C} ➔ {D}}
Le sous-ensemble I de S qui suit peut remplacer S puisqu'ils ont la même fermeture par rapport à R,
I
+ = S
+ :
I = {{A} ➔ {B}, {B,C} ➔ {D}}
R a pour seule clé candidate {A,C}, mais à cause de la DF {A} ➔ {B} la 2NF est violée.
Normalisons en mettant à profit le théorème de Heath. A partir de cette DF,
on produit deux relvars respectant la BCNF (clés soulignées) :
R1 {
A,B}, R2 {
A,
C,D} ;
Mais on perd la DF {B,C} ➔ {D} ce qui entraîne la mise en œuvre d'une contrainte
inter-relvars (cf. paragraphe 3.7).
Par exemple, R1 ayant pour corps {{a1, b1}, {a2, b1}} et R2 ayant pour corps
{{a1, c1, d1}, {a2, c1, d2}}, le corps de la jointure naturelle de R1 et R2
est égal à {{a1, b1, c1, d1}, {a2, b1, c1, d2}},
en contradiction avec {B,C} ➔ {D}.
Cherchons donc une décomposition meilleure. A partir de la DF {B,C} ➔ {D}
on peut décomposer R de la façon suivante :
R3 {
B,
C,D}, R4 {
A,
B,C} ;
Toutefois R4 viole à son tour la 2NF et l'on doit poursuivre le travail de normalisation, pour aboutir à :
R1 {
A,B}, R3 {
B,
C,D}, R5 {
A,
C} ;
Cette fois-ci la BCNF est respectée (ainsi d'ailleurs que
la 6NF), mais on
peut se poser la question de savoir si la DF {A,C} ➔ {D}
est préservée :
on peut
le prouver à l'aide d'un théorème
dont l'algorithme
qui l'accompagne est le suivant
(cf. [Ullman 1982],
« Algorithm 7.3 :
Testing
Preservation of Dependencies ») :
Z = X
while changes to Z occur
do
for i = 1 to k
do
Z = Z

((Z

R
i)
+

R
i)
A cet effet on définit d'abord un ensemble G qui est l'union des projections sur S de R1, R3 et R5 :
G =
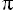 AB
AB(S)

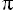 BCD
BCD(S)

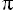 AC
AC(S)
Dans l'algorithme, X est le déterminant d'une DF X ➔ Y appartenant à S.
R
i représente successivement les éléments de la décomposition
ρ = (R1, R3, R5), à savoir {A,B}, {B,C,D} et {A,C}.
(Z

R
i)
+
est la fermeture de
(Z

R
i)
par rapport à S. En fin de parcours, si Y est un sous-ensemble de Z, alors
X ➔ Y appartient à G. Si chaque DF telle que
X ➔ Y appartenant à S appartient aussi à G, alors
ρ
préserve S, dans le cas contraire il y a perte de DF.
Dans notre cas, la DF dont on veut s'assurer de la préservation est {A,C} ➔ {D}.
On initialise Z avec le déterminant {A,C} de cette DF et R
i est successivement égal
à R1, R3 et R5 (puis R1 et R3 à nouveau s'il le faut).
Lors de la 1re itération, la situation évolue ainsi :
Z = {A,C}

(({A,C}

{A,B})
+

{A,B})
= {A,C}

({A}
+ 
{A,B})
= {A,C}

({A,B}

{A,B})
Car {A}
+ par rapport à S = {A,B}
= {A,C}

{A,B}
= {A,B,C}
Lors de la 2e itération, la situation évolue ainsi :
Z = {A,B,C}

(({A,B,C}

{B,C,D})
+

{B,C,D})
= {A,B,C}

({B,C}
+ 
{B,C,D})
= {A,B,C}

({B,C,D}

{B,C,D})
Car {B,C}
+ par rapport à S = {B,C,D}
= {A,B,C}

{B,C,D}
= {A,B,C,D}
Le dépendant {D} de la DF {A,C} ➔ {D} constitue un sous-ensemble de Z,
donc {A,C} ➔ {D} appartient à G. On montre de la même façon que les
DF {A ➔ {B} et {B,C} ➔ {D} appartiennent à G,
en conséquence de quoi la décomposition ({A,B}, {B,C,D}, {A,C}) est sans perte de DF.
 |
La décomposition d'une relvar peut très bien préserver les dépendances fonctionnelles mais pas
le contenu de la base de données. Reprenons l'exemple de la relvar R {A,B,C} dont l'ensemble de
dépendances fonctionnelles associé est S = {{A} ➔ {B}} (cf. paragraphe E.7.1).
On a montré que si l'on n'appliquait pas le théorème de Heath en décomposant R en R1 {A,B} et
R2 {B,C}, le contenu de la base données n'était pas préservé. Mais on peut facilement vérifier
que cette décomposition préserve la DF {A} ➔ {B}.
|
Reconsidérons maintenant la relvar R {A,B,C,D,E} (cf. paragraphe E.7.1) pour laquelle l'ensemble S
de DF associé est le suivant :
S = {{A} ➔ {C}, {B} ➔ {C},
{C} ➔ {D}, {D,E} ➔ {C}, {C,E} ➔ {A}}
Et la décomposition proposée est la suivante :
ρ = ({A,D}, {A,B}, {C,D,E}, {A,E}, {B,E})
Comme cette décomposition ne résulte pas de l'application du théorème de Heath, il est possible
que la préservation des DF ne soit pas assurée. Vérifions.
La DF {A} ➔ {C} est-elle préservée ? Commençons avec le 1er élément de
la décomposition, {A,D} :
Z = {A}

(({A}

{A,D})
+

{A,D})
= {A}

({A}
+ 
{A,D})
= {A}

({A,C,D}

{A,D})
Car {A}
+ par rapport à S = {A,C,D}
= {A}

{A,D}
= {A,D}
Poursuivons avec le 2e élément de la décomposition, {A,B} :
Z = {A,D}

(({A,D}

{A,B})
+

{A,B})
= {A,D}

({A}
+ 
{A,B})
= {A,D}

({A,C,D}

{A,B})
= {A,D}

{A}
= {A,D}
Z n'a pas évolué. Poursuivons avec le 3e élément de la décomposition, {C,D,E} :
Z = {A,D}

(({A,D}

{C,D,E})
+

{C,D,E})
= {A,D}

({D}
+ 
{C,D,E})
= {A,D}

({D}

{C,D,E})
Car {D}
+ par rapport à S = {D}
= {A,D}

{D}
= {A,D}
Z n'a pas évolué. Poursuivons avec le 4e élément de la décomposition, {A,E} :
Z = {A,D}

(({A,D}

{A,E})
+

{A,E})
= {A,D}

({A}
+ 
{A,E})
= {A,D}

({A,C,D}

{A,E})
= {A,D}

{A}
= {A,D}
Z n'a pas évolué. Poursuivons avec le 5e et dernier élément de la décomposition, {B,E} :
Z = {A,D}

(({A,D}

{B,E})
+

{B,E})
= {A,D}

(Ø

{B,E})
= {A,D}
Z ne peut plus évoluer et ne contient pas l'attribut C : la DF {A} ➔ {C} n'est pas préservée,
donc la décomposition
ρ ne préserve pas les DF.
E.8. Conclusion
Démontrer qu'une relvar R vérifie la BCNF passe en théorie
par le calcul de la fermeture {S}+ de R,
c'est-à-dire l'établissement de la liste complète des dépendances
fonctionnelles pouvant être inférées de l'ensemble donné S
des dépendances fonctionnelles vérifiées par R.
En fait, étant donné que l'on cherche fondamentalement à établir la liste des clés
candidates (donc a fortiori la liste des surclés) pour vérifier que les dépendances fonctionnelles
composant S n'entraînent pas un viol de BCNF, on peut éviter le calcul long et
particulièrement monotone de la fermeture. Il suffit en effet d'en passer par les solutions de
contournement très simples, grâce à l'utilisation de l'algorithme du seau et à la
technique du rouleau compresseur. On évite ainsi de s'énerver, tenter désespérément d'enchaîner les axiomes
d'Armstrong, et l'on fait des économies côté aspirine.
Par ailleurs, déterminer un sous-ensemble de S qui soit irréductible permet le cas
échéant de réduire au strict minimum le nombre de dépendances fonctionnelles composant S, donc les
contraintes que l'on demandera au système de garantir.
En réalité, dans tout cela, il est surtout à souhaiter que l'ensemble S des dépendances
fonctionnelles soit pertinent, c'est-à-dire que les règles de gestion des données
correspondantes, issues du travail de conception en amont soient les plus complètes
qu'il soit. Mais ceci est autre histoire...
Et tant qu'à faire, on s'assurera que les décompositions auxquelles on procède préservent
le contenu de la base de données ainsi que les dépendances fonctionnelles, en n'hésitant pas
à vérifier qu'il en est bien ainsi, en mettant à profit les algorithmes prévus à cet effet.
F. Identification relative versus identification absolue
F.1. Consommation des ressources physiques
Reprenons les tables utilisées pour illustrer l'alternative identification relative,
identification absolue (cf. paragraphe 1.7).
.png)
Figure F.1 - Identification relative et redondance intra-clés
.png)
Figure F.2 - Identification absolue
Picturalement parlant, dans le cas de l'identification absolue on a diminué le nombre d'attributs des tables,
mais en ce qui concerne la base de données, peut-on en conclure que cela entraîne une diminution de la volumétrie ?
Dans le cas de l'identification relative, la clé primaire de la table Livraison représente un encombrement
de 12 octets (4 octets, soit 232 valeurs pour l'attribut CliId et 2 octets,
soit 216 valeurs pour chaque autre attribut). Cette clé primaire contient la clé
étrangère relative à la table Engagement, clé étrangère qui ne représente donc aucun surcoût.
Dans le cas de l'identification absolue, la clé primaire {LivrId}
de la table Livraison représente
un encombrement de 4 octets, ce à quoi il faut ajouter 4 octets
pour la clé étrangère {EngId}
relative à la table Engagement. Arithmétiquement parlant, dans le cas de l'identification relative,
on a un surcoût de 4 octets : y a-t-il là de la gabegie ?
Quantifions maintenant la volumétrie au niveau des tables et des index et prenons l'exemple du SGBD
DB2 for z/OS Version 8 (à chacun d'effectuer les calculs en fonction de son SGBD). Partons sur la
base d'un million de clients, dix commandes en moyenne par client, etc., et faisons figurer les
volumétries correspondantes (exprimées en giga-octets). Concernant les index, ne figurent que ceux
qui nous intéressent, à savoir ceux qui sont imposés pour les clés primaires (PK) et ceux qui sont
nécessaires pour la performance des jointures entre clés primaires (PK) et étrangères (FK) :
Les index associés aux attributs correspondant à des points d'entrée à l'usage de l'utilisateur
(n° Siret, n° de commande, n° de bordereau de livraison, etc.) ne sont pas pris en compte
dans la mesure où ils ne jouent aucun rôle quant à la comparaison des coûts respectifs de
l'identification relative par rapport à l'identification absolue. Pour mémoire — à l'intention des DBA
qui comptent les accès au disque —, on a fait figurer le nombre de niveaux par index.
Figure F.3 - Coûts de stockage comparés
Paradoxalement, la volumétrie est moins importante dans le cas de l'identification relative.
Ceci est dû au fait que les index hébergeant les clés étrangères n'ont pas à être créés puisque
« phagocytés » par ceux qui hébergent les clés primaires ; et l'on pourrait pénaliser
l'identification absolue de près d'un Go supplémentaire si, en plus de la clé étrangère ciblant
la table « parente », la clé de chaque index « FK » comportait la clé primaire de
la table « fille » elle-même. Ainsi, l'intuition et certaines idées reçues
peuvent être prises en défaut...
F.2. Performance des applications
Selon les volumes de données brassés par les applications, l'utilisation de l'identification absolue
peut se révéler néfaste pour les performances. Dans le cas d'une transaction légère (Joe transaction
par référence à une bande dessinée bien connue), l'utilisateur n'est pas pénalisé (les tableaux de bord
de la Production informatique peuvent toutefois montrer une consommation globale élevée des ressources).
En revanche, le temps d'exécution d'une requête lourde (Jane Query) et surtout d'un bon batch
(Bill Batch) peuvent être très sensiblement pénalisés.
En effet, supposons que l'on ait besoin de savoir quels camions passeront chez quels clients.
Descendons dans la soute. Si on utilise l'identification relative, grâce à l'attribut commun
CliId on peut regrouper dans un même enregistrement sur le disque les commandes d'un client
(effet cluster au sens DB2, voir paragraphe F.3). Même chose pour les autres tables : les
lignes de chaque commande d'une commande d'un client donné se retrouvent dans un même enregistrement
du fichier hébergeant ces lignes de commande, etc. Pour un client donné, la lecture d'un enregistrement
physique de la table Livraison suffira (deux lectures si les données sont à cheval sur deux
enregistrements) pour obtenir ce que l'on cherche (outre trois lectures pour l'index associé qui comporte
quatre niveaux). Si un magasinier doit accéder aux livraisons à partir d'un numéro de bordereau de
livraison et qu'il a besoin des données concernant les clients à livrer, l'effet cluster continuera à jouer
pour la performance de la requête SQL correspondante.
Si on utilise l'identification absolue, pour arriver à une performance comparable en lecture,
on s'en sortira pour la table Commande en rendant cluster (au sens DB2 ou SQL Server) l'index utilisé
pour la clé étrangère {CliId}, mais dans le cas des tables suivantes on sera coincé (à noter qu'avec
l'identification relative, on sait que l'on fait l'économie d'un index, ce qui est nettement meilleur
pour la performance des mises à jour des tables). Les bienfaits du clustering sont détaillés dans
l'annexe suivante (contexte DB2 for z/OS, mais ceci vaut vraisemblablement pour d'autres SGBD tels
que SQL Server déjà cité).
F.3. Le clustering selon DB2 for z/OS
Depuis sa naissance (1983), DB2 permet le regroupement et le rangement physiques (clustering)
des lignes d'une table selon une séquence qui est celle de la clé d'un index en particulier.
Prenons le cas de la table Commande (cf. paragraphe 1.7, 4e exemple) : Nous voudrions regrouper
toutes les commandes d'un client dans une même page (ou un minimum de pages physiquement adjacentes
s'il y a beaucoup de commandes pour le client), afin de réduire le plus possible le nombre d'accès
au disque pour manipuler tout ou partie de ces commandes. Le clustering sera effectué en fonction
d'une clé qui en l'occurrence sera constituée de l'attribut CliId, servant à référencer la table
Client (de clé primaire {CliId}).
Supposons que tel jour on a créé successivement des commandes pour les clients 12345, 40364, 00012, etc.,
logées par le SGBD dans les pages consécutives p1, p2, etc.,
à raison — pour fixer les idées — de 80 commandes par page.

Figure F.4 - Hébergement physique des commandes
Les jours passant, si l'on crée une 2e commande pour le client 12345, celle-ci se trouvera dans
une page pi probablement fort éloignée de la page p1. Si donc on exécute
une requête pour obtenir l'ensemble des commandes de ce client, il y aura deux accès au disque,
un par commande, soit un coût de l'ordre de 10 millisecondes x 2 (sans tenir compte du surcoût
lié à l'index). Au pire, la création de n commandes pour ce client peut se traduire par un coût
d'accès de l'ordre de 10n millisecondes, pour peu que ses commandes se retrouvent
toutes dans des pages différentes.
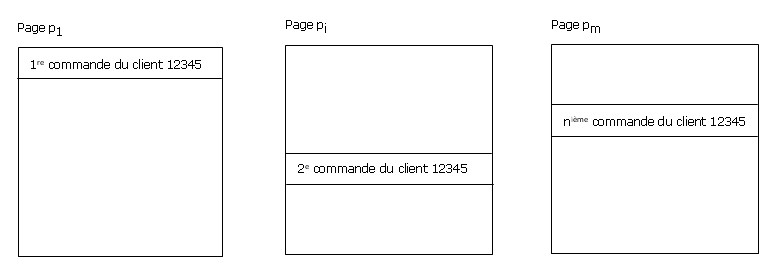
Figure F.5 - Éparpillement des commandes
Notre objectif est donc de faire en sorte que le SGBD regroupe les commandes d'un client
dans une même page. Techniquement parlant, cela implique la mise en œuvre d'un
index — dit cluster — parmi l'ensemble des index associés à la table des commandes
(en l'occurrence l'index qui sert pour la clé étrangère par rapport à la table Client).
A cet effet, on dotera la table Commande d'un tel index :
CREATE INDEX Commandex1 (CliId, CdeId) ON Commande CLUSTER ... ;
En conséquence de quoi, le contenu de la page p1 devrait théoriquement devenir le suivant :

Figure F.6 - Regroupement des commandes dans une même page
Mais il est évident que le client 12345 n'a pas l'exclusivité de la page p1 et s'il passe sa 2e commande
longtemps après la 1re, cette page ne pourra pas l'héberger, car contenant des commandes passées entre
temps par d'autres clients. C'est pourquoi le DBA surveille les statistiques fournies par le catalogue
relationnel qui permettent de savoir si l'effet cluster est effectif (cluster ratio) :
au besoin, il procède à la réorganisation du table space hébergeant la table Commande,
suite à quoi le clustering sera respecté à 100% (au moins pour un temps). A noter que l'on peut
imposer à cette occasion que soit gelé un certain pourcentage de place libre (free space), récupérable
seulement pour les INSERT à venir, et, tant qu'il trouvera de la place encore libre, DB2 essaiera alors
d'insérer chaque nouvelle commande d'un client donné dans la page contenant celles que celui-ci a déjà passées.
Quoi qu'il en soit, suite à réorganisation, les n commandes d'un client seront regroupées dans
la même page et le coût pour les lire ne sera plus de l'ordre de 10n millisecondes, mais plutôt
de 10 millisecondes (plus environ 0,0004*(p-1) millisecondes si les n commandes occupent
p pages adjacentes, la constante 0,0004 représentant le coût d'un accès séquentiel supplémentaire
pour des disques de type IBM ESS).
Toutes choses égales par ailleurs, ce qui vaut pour les commandes vaut aussi pour les tables qui en dépendent
directement ou non (table des lignes de commande, celle des engagements et celle des livraisons).
Cas de la table Client
Ce qui vaut pour la table Commande ne vaut pas pour la table Client, à savoir vouloir faire du clustering
basé sur l'attribut CliId, au contraire. En effet, autant le regroupement des commandes d'un client se
justifie d'un point de vue sémantique, ontologique, puis physique, autant le regroupement des clients
sur un quelconque critère ne vaut pas (du moins intuitivement) : en effet, de quel objet les clients
seraient-ils donc des propriétés multivaluées ? Seul un examen du fonctionnel, en relation avec le
chef de projet de l'application, pourra guider le DBA pour mettre en évidence un critère intéressant
du point de vue fonctionnel et qui permette de réduire la durée des traitements lourds (Bill Batch,
Jane Query). A défaut, au moins dans le cas de DB2 — pour lequel existe exactement un index
cluster par table —, on se servira d'un index autre que l'index primaire (de clé CliId), afin d'éviter
des phénomènes de verrouillage (histoire vécue). Par exemple, si l'on retient pour être cluster
l'index permettant à l'utilisateur d'accéder directement aux clients par leur numéro Siret, on a peu de
risques de provoquer des verrouillages car, en cas de création simultanée et intensive de clients lors
de transactions concurrentes, on a droit à un mécanisme de hachage naturel, provoquant un éparpillement
bienvenu des clients dans les pages physiques. Cet éparpillement vaut non seulement pour la table Client,
mais aussi pour la table Commande et pour sa descendance (du fait du 1er attribut de la clé,
à savoir CliId), sans pour autant remettre en cause le clustering des commandes d'un client,
donc la performance des traitements lourds.
Le rôle crucial de l'index cluster. I/O bound vs CPU bound.
Si un programme calcule le nombre PI avec des millions de décimales, le processeur sera très fortement
mis à contribution, mais pas le disque. Dans le jargon, on dit que ce programme est CPU bound
(Compute bound ou Central Processing Unit bound, selon les lieux et époques) :
la durée du traitement dépend de la puissance du processeur.
A l'opposé, il est un problème auquel sont confrontés pratiquement en permanence les DBA :
celui de la lenteur de certaines transactions ou traitements lourds (encore Jane Query et Bill Batch)
accédant à de grands volumes de données, auquel cas la durée du traitement est tributaire de la
performance du disque ; toujours dans le jargon, on dit alors que le programme est
I/O bound (Input/Output bound) ou encore I/O Wait.
Supposons par exemple que l'on ait une table CLIENT de 10 millions de lignes, accompagnée d'une
table ADRESSE de 15 millions de lignes (un client peut avoir plus d'une adresse, telle qu'une
adresse de facturation en plus de son adresse de domiciliation, et encore
d'autres adresses pour d'autres usages).
Structure des tables :
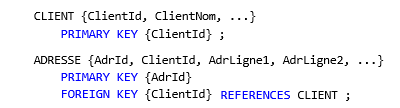
Supposons encore que l'on ait à effectuer la jointure (naturelle) de ces deux tables. Selon la syntaxe SQL :

Si l'index cluster de la table Adresse a pour clé {AdrId}, à l'analyse des résultats on constatera que
le processeur aura très peu travaillé et l'on aurait utilisé un processeur trois fois plus puissant
que cela n'aurait pratiquement rien changé quant à la durée elapsed (horloge) ; en revanche, le
système aura été en permanence en attente de fin des opérations de lecture sur le disque à l'origine
d'un phénomène d'I/O Wait fort mal venu, avec une durée globale du traitement que l'on aurait
volontiers vue divisée par un facteur très important...
Voici un exemple de simulation faite avec l'outil DB2 Estimator d'IBM. On a choisi le SGBD DB2 for z/OS
version 8, un processeur de puissance modeste, à savoir un IBM 9672 Y16 (150 mips, 500 Mhz).
Les disques sont des ESS-F20 (15 000 tours/minute). La lecture d'une page de 4K consomme 0,0004 sec.
en mode séquentiel, de 0,005 à 0,010 sec. en mode aléatoire.
Coût de la requête suivante :

Premier scénario : A la clé étrangère {ClientId} de la table ADRESSE on associe un index
non cluster. La taille d'une ligne est en moyenne de 140 octets (avant compression à 80%).
|
Coûts estimés par l'outil :
CPU Time = 00:32:23 ; I/O Time = 20:50:17 ;
Min. Elapsed Time = 21:22:23.
Ainsi, faut-il compter plus de 20 heures avant que la requête ne se termine, du fait des accès au disque
(lectures synchrones).
Pour réaliser la tâche, DB2 utilise la technique bien connue des DBA, dite du Nested loop (boucle imbriquée).
DB2 utilise des techniques permettant de réduire assez sensiblement le coût des lectures synchrones, telles que
celle du List prefetch, mais que nous ne pouvons pas aborder ici.
|
Deuxième scénario : L'index est rendu cluster :
|
Coûts estimés : CPU Time = 00:17:21 ;
I/O Time = 00:01:20 ;
Min. Elapsed Time = 00:17:21.
Cette fois-ci, les accès au disque ne sont plus en cause, leur coût a été divisé par un facteur supérieur
à 900, on n'est plus I/O bound, mais CPU bound : au besoin, et si on a le budget pour, la durée
elapsed pourra être réduite en augmentant la puissance du processeur.
Là encore, DB2 utilise la technique du Nested loop.
|
Troisième scénario : Si l'index n'est pas cluster et si on peut le supprimer avant l'exécution
de la requête (pour le recréer après, cf. au paragraphe 3.8 le coup de la suppression des chèques),
DB2 n'utilise plus la technique du Nested loop mais celle
du Merge scan (à la façon de l'appareillage de fichiers).
Dans ces conditions, les coûts estimés sont les suivants :
|
CPU Time = 00:17:17 ; I/O Time = 00:08:48 ; Min. Elapsed Time = 00:25:27.
Cette solution est loin d'être inintéressante. (Sans supprimer l'index, on peut aussi demander à
DB2 d'utiliser la technique du Merge scan pour la requête).
|
Cas des prestations.
Supposons que la table CLIENT soit en relation avec une table de prestations des clients
(comparable à celle des adresses quant à la taille d'une ligne et au pourcentage de compression),
mais cette fois-ci pour une volumétrie de 80 000 000 de lignes.
Coût de la requête suivante :

Premier scénario : A la clé étrangère {ClientId} de la table PRESTATION on associe un index
non cluster :
L'emploi par DB2 de la technique du Nested loop donne lieu à des résultats catastrophiques,
plus de 4 jours avant d'obtenir le résultat (des disques tournant à 100 000 tours/minute
ne seraient pas d'un grand secours..., par contre, forcer DB2 à utiliser le Merge scan peut
sauver la situation, ce qui est aussi possible s'il se sert du list prefetch, en stockant
en mémoire les pointeurs (triés) vers les 1 000 000
de pages occupées par les 80 000 000 de prestations) :
Coûts estimés : CPU Time = 02:29:21 ;
I/O Time = 111:07:30 ;
Min Elapsed Time = 113:36:01
Deuxième scénario : Si l'index est rendu cluster :
Coûts estimés : CPU Time = 01:09:08 ;
I/O Time = 00:03:45 ;
Min Elapsed Time = 01:09:08
Là encore les accès au disque ne sont plus en cause, on n'est plus I/O bound, mais bien
CPU bound : une fois de plus, si cela est jugé nécessaire et si l'on a les budgets,
le coût pourra être réduit en augmentant la puissance du processeur.
Conclusions
Dans le cas des traitements de masse, l'identification absolue a de fortes chances de causer de
gros problèmes de performance. Les résultats présentés ne sont que les estimations de DB2 Estimator
et, en situation réelle, il faudrait effectuer un EXPLAIN pour vérifier si DB2 utilise la technique
du Merge scan (certes coûteuse en ressources du fait de tris inhérents) ou celle du Nested loop qui
peut se révéler funeste. Et au-delà de DB2 for z/OS, cela vaut évidemment quel que soit le SGBD.
Le choix de l'index cluster est déterminant pour la performance de ce type de traitements pour
lesquels on accède à un nombre élevé de pages physiques, et autant on pourra arriver à réduire les
durées en cas de CPU bound en augmentant la puissance du processeur, autant cela sera vraisemblablement
vain en cas d'I/O bound, sauf à forcer DB2 à utiliser un Merge scan ou encore si celui-ci met en œuvre
un list prefetch efficace, avec stockage en mémoire des pointeurs (triés) vers 1 000 000
de pages occupées par 80 000 000 de prestations, sans compter une cinquantaine d'autres
tables de volumétrie comparable, compressées elles aussi au maximum.
 |
La modélisation conceptuelle peut être impactée : il s'agit de l'alternative identification
absolue vs identification relative : Pour reprendre l'exemple des clients et des commandes,
si l'on s'en tient à l'identification absolue, on pourra rendre cluster non pas l'index primaire
de la table COMMANDE mais celui qui sert pour la clé étrangère {CliId}, néanmoins on sera coincé
quant à la performance des accès à la table des lignes de commande, le phénomène d'I/O bound
réapparaissant inévitablement, hélas.
|
Et concernant l'incantation « la jointure ça coûte cher, donc il faut dénormaliser », voilà
encore une légende à détruire... On peut dire que le coût de la jointure dépend très
fortement de nos choix de modélisation conceptuelle et physique. Et, Last but not least,
pour en revenir à notre sujet, n'oublions pas que la jointure est au coeur de la normalisation
comme l'illustre le théorème de Heath (cf. paragraphe 3.3.2).
F.4. L'identification relative au service de l'intégrité des données
L'identification relative présente des avantages variés. Je reprends ici une discussion que l'on peut retrouver chez
DVP.
On traite des offres concernant des véhicules automobiles. Un des buts de la manœuvre est d'interdire
par exemple que l'on associe une offre Renault à une motorisation Peugeot ou à une finition Citroën...
1er cas de figure. On utilise l'identification absolue. Le MLD est le suivant (clés primaires soulignées,
clés étrangères en italiques) :
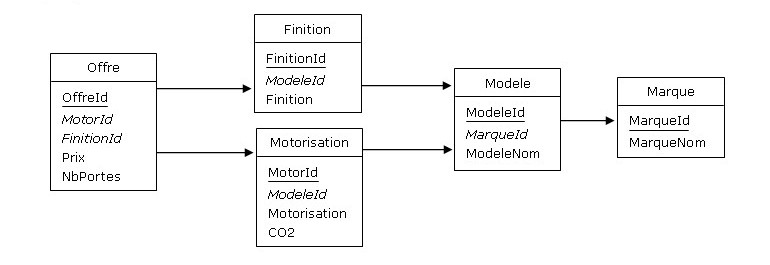
Figure F.7 - Offres - Identification absolue
Pour éviter les erreurs, il faudra programmer un trigger garantissant la cohérence des données.
2e cas de figure. On utilise l'identification relative. Le MLD devient le suivant :
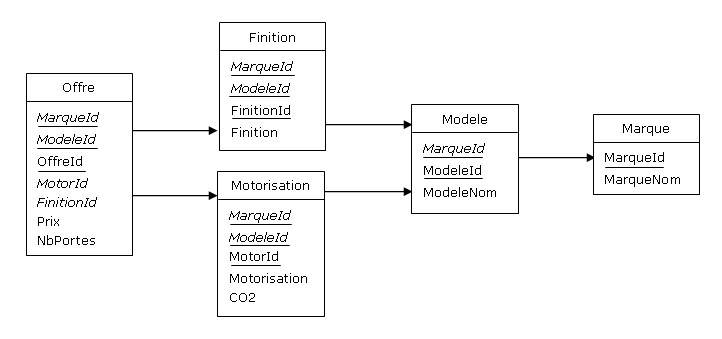
Figure F.8 - Offres - Identification relative
Du fait de l'identification relative (en association avec l'intégrité référentielle),
il n'y a plus besoin de programmer un quelconque trigger pour s'assurer qu'une offre sera
cohérente avec la marque, car l'attribut MarqueId est propagé jusqu'à la table Offre.
Ainsi, chaque ligne de la table Offre prenant la valeur "Renault" pour l'attribut MarqueId
ne peut faire référence qu'à une ligne de la table Finition prenant elle aussi la valeur
"Renault" pour l'attribut MarqueId (intégrité référentielle oblige). A son tour, cette
ligne de la table Finition ne peut faire référence qu'à une ligne de la table Modele prenant
elle aussi la valeur "Renault" pour l'attribut MarqueId (intégrité référentielle oblige une
fois de plus). A son tour, cette ligne de la table Modele ne peut faire référence qu'à une
ligne de la table Marque prenant elle aussi la valeur "Renault" pour l'attribut MarqueId
(intégrité référentielle, encore et encore). Ce qui vaut pour les liens qui unissent
Offre et Finition vaut évidemment pour Offre et Motorisation.


Copyright © 2008 - François de Sainte Marie.
Aucune reproduction, même partielle, ne peut être faite
de ce site ni de l'ensemble de son contenu : textes, documents, images, etc.
sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à
trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.









.jpg)
.jpg)
.png)





3lignes.jpg)

3lignes.jpg)
indente.jpg)
indente.jpg)
.jpg)
3lignes.jpg)
.png)
.png)
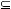 V
V
 Y
Y
 {A,B} ➔ {A} (réflexivité) ;
{A,B} ➔ {A} (réflexivité) ;
 La DF {A} ➔ {B,C} est donnée, donc par transitivité on produit la DF
{A,B} ➔ {B,C} ;
La DF {A} ➔ {B,C} est donnée, donc par transitivité on produit la DF
{A,B} ➔ {B,C} ;
 Et par augmentation : {A,B} ➔ {A,B,C}.
Et par augmentation : {A,B} ➔ {A,B,C}.
 {A,B,C} ➔ {B} (réflexivité) ;
{A,B,C} ➔ {B} (réflexivité) ;
 La DF {B} ➔ {E} est donnée, donc par transitivité on produit la DF
{A,B,C} ➔ {E} ;
La DF {B} ➔ {E} est donnée, donc par transitivité on produit la DF
{A,B,C} ➔ {E} ;
 Et par augmentation, {A,B,C} ➔ {A,B,C,E}.
Et par augmentation, {A,B,C} ➔ {A,B,C,E}.
50pc.jpg) {B,C,D,E,G}, etc.
{B,C,D,E,G}, etc.
3lignes.jpg)
3lignes.jpg)
3lignes.jpg)

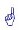
3lignes.jpg)
 R2) ➔ (R1 — R2)
ou
(R1
R2) ➔ (R1 — R2)
ou
(R1  R2) ➔ (R2 — R1).
R2) ➔ (R2 — R1).
 {A,C} = {A}
et d'autre part
{A,B} — {A,C} = {B}, donc on vérifie bien {A} ➔ {B}.
{A,C} = {A}
et d'autre part
{A,B} — {A,C} = {B}, donc on vérifie bien {A} ➔ {B}.
 {B,C} = {B},
{A,B} — {B,C} = {A} et {B,C} — {A,B} = {C} :
(R1
{B,C} = {B},
{A,B} — {B,C} = {A} et {B,C} — {A,B} = {C} :
(R1  R2) ne détermine fonctionnellement
ni (R1 — R2) ni (R2 — R1), le contenu de la base de données n'est
donc pas préservé. On peut du reste le vérifier à l'aide d'un exemple :
R2) ne détermine fonctionnellement
ni (R1 — R2) ni (R2 — R1), le contenu de la base de données n'est
donc pas préservé. On peut du reste le vérifier à l'aide d'un exemple :
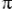 AB(r) et
R2 =
AB(r) et
R2 = 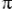 BC(r)
sont respectivement égales à {{a1,b1}, {a2,b1}} et {{b1,c1}, {b1,c2}}
tandis que leur jointure naturelle est égale à
{{a1,b1,c1}, {a1,b1,c2}, {a2,b1,c1}, {a2,b1,c2}}, laquelle n'est pas égale à r.
BC(r)
sont respectivement égales à {{a1,b1}, {a2,b1}} et {{b1,c1}, {b1,c2}}
tandis que leur jointure naturelle est égale à
{{a1,b1,c1}, {a1,b1,c2}, {a2,b1,c1}, {a2,b1,c2}}, laquelle n'est pas égale à r.






 ((Z
((Z  Ri)+
Ri)+
 Ri)
Ri)
 AB(S)
AB(S)

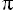 BCD(S)
BCD(S)

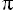 AC(S)
AC(S)
 Ri)+
est la fermeture de
(Z
Ri)+
est la fermeture de
(Z  Ri)
par rapport à S. En fin de parcours, si Y est un sous-ensemble de Z, alors
X ➔ Y appartient à G. Si chaque DF telle que
X ➔ Y appartenant à S appartient aussi à G, alors ρ
préserve S, dans le cas contraire il y a perte de DF.
Ri)
par rapport à S. En fin de parcours, si Y est un sous-ensemble de Z, alors
X ➔ Y appartient à G. Si chaque DF telle que
X ➔ Y appartenant à S appartient aussi à G, alors ρ
préserve S, dans le cas contraire il y a perte de DF.
 (({A,C}
(({A,C}  {A,B})+
{A,B})+
 {A,B})
{A,B})
 ({A}+
({A}+  {A,B})
{A,B})
 ({A,B}
({A,B}  {A,B})
Car {A}+ par rapport à S = {A,B}
{A,B})
Car {A}+ par rapport à S = {A,B}
 {A,B}
{A,B}
 (({A,B,C}
(({A,B,C}  {B,C,D})+
{B,C,D})+
 {B,C,D})
{B,C,D})
 ({B,C}+
({B,C}+  {B,C,D})
{B,C,D})
 ({B,C,D}
({B,C,D}  {B,C,D})
Car {B,C}+ par rapport à S = {B,C,D}
{B,C,D})
Car {B,C}+ par rapport à S = {B,C,D}
 {B,C,D}
{B,C,D}
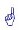
 (({A}
(({A}  {A,D})+
{A,D})+
 {A,D})
{A,D})
 ({A}+
({A}+  {A,D})
{A,D})
 ({A,C,D}
({A,C,D}  {A,D})
Car {A}+ par rapport à S = {A,C,D}
{A,D})
Car {A}+ par rapport à S = {A,C,D}
 {A,D}
{A,D}
 (({A,D}
(({A,D}  {A,B})+
{A,B})+
 {A,B})
{A,B})
 ({A}+
({A}+  {A,B})
{A,B})
 ({A,C,D}
({A,C,D}  {A,B})
{A,B})
 {A}
{A}
 (({A,D}
(({A,D}  {C,D,E})+
{C,D,E})+
 {C,D,E})
{C,D,E})
 ({D}+
({D}+  {C,D,E})
{C,D,E})
 ({D}
({D}  {C,D,E})
Car {D}+ par rapport à S = {D}
{C,D,E})
Car {D}+ par rapport à S = {D}
 {D}
{D}
 (({A,D}
(({A,D}  {A,E})+
{A,E})+
 {A,E})
{A,E})
 ({A}+
({A}+  {A,E})
{A,E})
 ({A,C,D}
({A,C,D}  {A,E})
{A,E})
 {A}
{A}
 (({A,D}
(({A,D}  {B,E})+
{B,E})+
 {B,E})
{B,E})
 (Ø
(Ø  {B,E})
{B,E})
.png)
.png)










